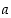 ja
ja 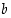 on olemassa sellainen luonnollinen luku
on olemassa sellainen luonnollinen luku 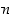 ,
että
,
että 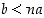 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Toteamme seuraavaksi, miksi on olemassa mielivaltaisen isoja kokonaislukuja ja mielivaltaisen pieniä positiivisia murtolukuja.
Lause 1.3.14. (Arkhimedeen laki)
Kaikille positiivisille reaaliluvuille 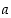 ja
ja 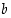 on olemassa sellainen luonnollinen luku
on olemassa sellainen luonnollinen luku 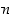 ,
että
,
että 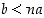 .
.
Todistus. Oletetaan, että vaadittua luonnollista lukua 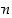 ei ole olemassa. Silloin
ei ole olemassa. Silloin 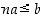 kaikilla luonnollisilla luvuilla, joten joukko
kaikilla luonnollisilla luvuilla, joten joukko 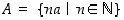 on ylhäältä rajoitettu. Joukolla
on ylhäältä rajoitettu. Joukolla 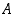 on näin ollen pienin yläraja
on näin ollen pienin yläraja 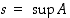 . Jos jokaiseen joukon
. Jos jokaiseen joukon 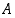 lukuun lisätään luku
lukuun lisätään luku 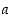 ,
niin näin saadulle joukolle
,
niin näin saadulle joukolle 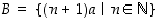 ovat sen ylärajat luvun
ovat sen ylärajat luvun 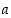 verran suurempia kuin joukon
verran suurempia kuin joukon 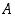 ylärajat. Siten myös
ylärajat. Siten myös 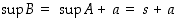 . Toisaalta joukossa
. Toisaalta joukossa 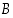 on nollaa lukuunottamatta samat luvut kuin joukossa
on nollaa lukuunottamatta samat luvut kuin joukossa 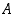 ,
joten
,
joten 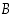 on joukon
on joukon 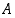 osajoukko. Siten ilman muuta
osajoukko. Siten ilman muuta 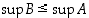 . On saatu ristiriitainen tilanne
. On saatu ristiriitainen tilanne 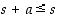 ,
joten vastaoletuksemme ei voi päteä, vaan haluttu luku
,
joten vastaoletuksemme ei voi päteä, vaan haluttu luku 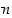 täytyy olla olemassa.
täytyy olla olemassa.
Arkhimedeen lauseella on seuraavat kaksi yksinkertaisen ja selvän tuntuista tosiasiaa. Ne ovat kuitenkin tärkeitä huomioita niitä tilanteita varten, joissa joudutaan tarkastelemaan oikein suuria tai oikein pieniä positiivisia lukuja.
(a) Luonnollisten lukujen joukko 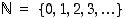 ei ole ylhäältä rajoitettu, ts. jokaiselle reaaliluvulle
ei ole ylhäältä rajoitettu, ts. jokaiselle reaaliluvulle 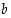 on olemassa luonnollinen luku
on olemassa luonnollinen luku 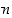 ,
jolle
,
jolle 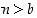 .
.
(b) Jokaiselle positiiviselle reaaliluvulle 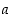 on olemassa sellainen luonnollinen luku
on olemassa sellainen luonnollinen luku 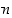 ,
että
,
että 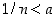 .
.
Todistus. Kohta (a) seuraa Arkhimedeen laista valitsemalla 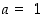 ja kohta (b) seuraa samasta laista valitsemalla vuorostaan
ja kohta (b) seuraa samasta laista valitsemalla vuorostaan 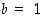 .
.
Ensinnäkin voidaan huomata, että luvusta 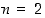 alkaen luvut
alkaen luvut 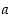 ovat positiivisia, joten
ovat positiivisia, joten 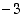 on joukon
on joukon 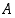 pienin luku ja samalla sen infimum.
pienin luku ja samalla sen infimum.
Onko 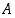 ylhäältä rajoitettu? Koska
ylhäältä rajoitettu? Koska
on luku 2 joukon 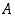 eräs yläraja. Se on siten ylhäältä rajoitettu joukko.
eräs yläraja. Se on siten ylhäältä rajoitettu joukko.
Onko joukolla 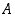 pienintä ylärajaa? Koska edellä olevassa arviossa poisjätetyt termit
pienintä ylärajaa? Koska edellä olevassa arviossa poisjätetyt termit 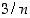 ja
ja 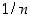 ovat luvun
ovat luvun 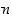 isoilla arvoilla pieniä, voi epäillä, että luku 2 olisi myös pienin yläraja. Olkoon tämän todistamista varten
isoilla arvoilla pieniä, voi epäillä, että luku 2 olisi myös pienin yläraja. Olkoon tämän todistamista varten 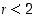 . Etsitään sellainen kokonaisluku
. Etsitään sellainen kokonaisluku 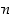 ,
että sitä vastaava
,
että sitä vastaava 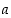 olisi suurempi kuin
olisi suurempi kuin 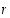 . Tehdään seuraava päättelyketju:
. Tehdään seuraava päättelyketju:
(viimeisin epäyhtälö pätee, koska 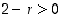 ). Valitsemalla
). Valitsemalla 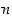 niin suureksi, että saatu ehto toteutuu, löydetään
niin suureksi, että saatu ehto toteutuu, löydetään 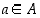 ,
jolle
,
jolle 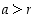 . Tällaisen luvun
. Tällaisen luvun 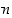 valinta on seurauslauseen 1.3.15 mukaan mahdollista. Yläraja 2 on siten pienin mahdollinen eli
valinta on seurauslauseen 1.3.15 mukaan mahdollista. Yläraja 2 on siten pienin mahdollinen eli 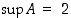 .
.
Opiskelutehtävä 4. (Supremum ja infimum)
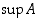 ,
,
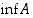 ,
,
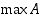 ja
ja 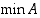 (jos ne ovat olemassa).
(jos ne ovat olemassa).