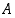 otetaan käyttöön seuraavat järjestykseen liittyvät nimitykset:
otetaan käyttöön seuraavat järjestykseen liittyvät nimitykset:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Reaalilukujen osajoukoille 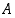 otetaan käyttöön seuraavat järjestykseen liittyvät nimitykset:
otetaan käyttöön seuraavat järjestykseen liittyvät nimitykset:
• Joukolla 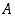 on ylärajana luku
on ylärajana luku 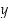 ,
jos
,
jos 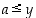 kaikille
kaikille 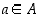 .
.
• Joukolla 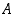 on alarajana luku
on alarajana luku 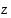 ,
jos
,
jos 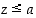 kaikille
kaikille 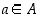 .
.
• Joukko 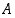 on ylhäältä rajoitettu,
jos sillä on yksikin yläraja. Vastaavasti se on alhaalta rajoitettu,
jos sillä on yksikin alaraja. Joukko
on ylhäältä rajoitettu,
jos sillä on yksikin yläraja. Vastaavasti se on alhaalta rajoitettu,
jos sillä on yksikin alaraja. Joukko 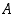 on rajoitettu, jos se on sekä ylhäältä että alhaalta rajoitettu.
on rajoitettu, jos se on sekä ylhäältä että alhaalta rajoitettu.
• Joukolla 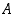 on suurin alkio
on suurin alkio 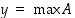 ,
jos se on joukon
,
jos se on joukon 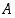 alkio, joka on kaikkia muita joukon
alkio, joka on kaikkia muita joukon 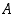 alkioita suurempi (jos niitä on), ts. jos
alkioita suurempi (jos niitä on), ts. jos 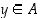 ja
ja 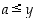 kaikille
kaikille 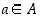 .
.
• Joukolla 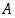 on pienin alkio
on pienin alkio 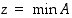 ,
jos se on joukon
,
jos se on joukon 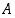 alkio, joka on kaikkia muita joukon
alkio, joka on kaikkia muita joukon 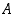 alkioita pienempi (jos niitä on), ts. jos
alkioita pienempi (jos niitä on), ts. jos 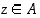 ja
ja 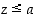 kaikille
kaikille 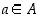 .
.
• Joukolla 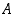 on pienin yläraja eli supremum
on pienin yläraja eli supremum 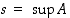 ,
jos se on joukon
,
jos se on joukon 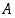 ylärajojen muodostaman joukon pienin alkio.
ylärajojen muodostaman joukon pienin alkio.
• Joukon 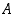 on suurin alaraja eli infimum
on suurin alaraja eli infimum 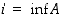 ,
jos se on joukon
,
jos se on joukon 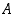 alarajojen muodostaman joukon suurin alkio.
alarajojen muodostaman joukon suurin alkio.
Välttämättä annettuun osajoukkoon ei liity edellä mainittuja alkioita ollenkaan tai sillä ei ole edellä mainittuja (rajoittuneisuus)ominaisuuksia.
Luonnollisten lukujen joukko 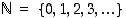 on alhaalta rajoitettu. Alarajaksi kelpaa mikä tahansa negatiivinen luku sekä nolla. Näistä suurin on nolla, joten
on alhaalta rajoitettu. Alarajaksi kelpaa mikä tahansa negatiivinen luku sekä nolla. Näistä suurin on nolla, joten 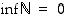 .
.
Joukon 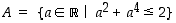 alkioille pätee, että
alkioille pätee, että 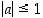 . Jos nimittäin
. Jos nimittäin 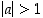 ,
on
,
on 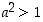 ja
ja 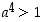 ,
joten myös
,
joten myös 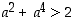 . Joukko
. Joukko 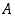 on siten rajoitettu (alhaalta luvulla
on siten rajoitettu (alhaalta luvulla 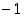 ja ylhäältä luvulla
ja ylhäältä luvulla 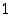 ).
).
Toisaalta jokainen luku 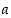 ,
jolle
,
jolle 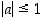 ,
toteuttaa ehdon
,
toteuttaa ehdon 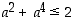 ,
joten se kuuluu joukkoon
,
joten se kuuluu joukkoon 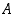 . Siten joukossa
. Siten joukossa 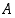 ovat täsmälleen ne luvut
ovat täsmälleen ne luvut 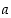 ,
joille on voimassa ehto
,
joille on voimassa ehto 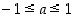 . Erityisesti
. Erityisesti 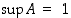 ja
ja 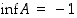 .
.
Joukko 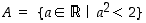 on ylhäältä rajoitettu luvulla 2. Jos nimittäin
on ylhäältä rajoitettu luvulla 2. Jos nimittäin 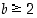 ,
on
,
on 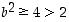 ,
joten
,
joten 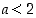 kaikilla
kaikilla 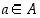 . Onko olemassa pienintä ylärajaa
. Onko olemassa pienintä ylärajaa 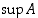 ? Vastaus selviää esimerkissä 1.3.13.
? Vastaus selviää esimerkissä 1.3.13.
Seuraava huomio auttaa usein pienimmän ylärajan selvittämisessä.
Reaalilukujen osajoukolle 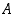 on
on 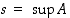 täsmälleen silloin, kun
täsmälleen silloin, kun
(2) jokaiselle 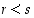 on olemassa jokin
on olemassa jokin 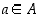 ,
jolle
,
jolle 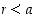 .
.
Todistus. Oletetaan ensin, että 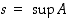 ja osoitetaan, että ehdot (1) ja (2) toteutuvat. Luku
ja osoitetaan, että ehdot (1) ja (2) toteutuvat. Luku 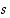 on nyt eräs joukon
on nyt eräs joukon 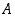 yläraja, joten ehto (1) toteutuu. Jos sitten ehto (2) ei toteutuisi, niin jollekin luvulle
yläraja, joten ehto (1) toteutuu. Jos sitten ehto (2) ei toteutuisi, niin jollekin luvulle 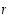 olisi
olisi 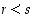 mutta ei olisi olemassa lukua
mutta ei olisi olemassa lukua 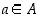 ,
jolle
,
jolle 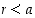 . Tällöin kaikilla
. Tällöin kaikilla 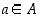 olisi
olisi 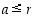 ,
joten myös luku
,
joten myös luku 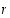 kelpaisi joukon
kelpaisi joukon 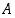 ylärajaksi. Se olisi siten pienempi yläraja kuin
ylärajaksi. Se olisi siten pienempi yläraja kuin 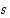 vastoin sen määrittelyä. Näin ollen myös ehto (2) toteutuu.
vastoin sen määrittelyä. Näin ollen myös ehto (2) toteutuu.
Oletetaan sitten, että luku 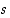 toteuttaa ehdot (1) ja (2). Silloin ehdon (1) mukaan
toteuttaa ehdot (1) ja (2). Silloin ehdon (1) mukaan 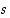 on yläraja. Pitää osoittaa vielä, että se on niistä pienin. Olkoon sitä varten
on yläraja. Pitää osoittaa vielä, että se on niistä pienin. Olkoon sitä varten 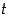 toinen joukon
toinen joukon 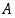 yläraja. Osoitetaan, että
yläraja. Osoitetaan, että 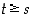 . Jos olisi
. Jos olisi 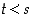 ,
olisi ehdon (2) mukaan olemassa jokin
,
olisi ehdon (2) mukaan olemassa jokin 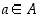 ,
jolle
,
jolle 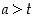 . Mutta silloinhan
. Mutta silloinhan 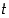 ei voisi olla joukon
ei voisi olla joukon 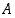 yläraja. On siis
yläraja. On siis 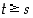 ,
mikä osoittaa sen, että
,
mikä osoittaa sen, että 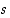 pienin joukon
pienin joukon 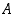 ylärajoista.
ylärajoista.
Kuten todistuksesta ilmenee, edellä olevan lauseen ensimmäinen ehto ilmaisee sen, että luku 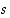 on joukon
on joukon 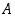 yläraja, ja toinen sen, että se on kaikista ylärajoista pienin.
yläraja, ja toinen sen, että se on kaikista ylärajoista pienin.
Vastaavasti voidaan todentaa seuraava tulos.
Reaalilukujen osajoukolle 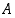 on
on 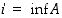 täsmälleen silloin, kun
täsmälleen silloin, kun
(2) jokaiselle 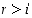 on olemassa joku
on olemassa joku 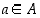 ,
jolle
,
jolle 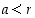 .
.
Edellisten tulosten perusteella havaitaan myös seuraavat tosiasiat.
Jos reaalilukujen osajoukolla 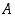 on suurin alkio
on suurin alkio 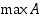 ,
on se samalla pienin yläraja
,
on se samalla pienin yläraja 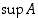 . Vastaavasti, jos reaalilukujen osajoukolla
. Vastaavasti, jos reaalilukujen osajoukolla 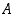 on pienin alkio
on pienin alkio 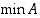 ,
on se samalla suurin alaraja
,
on se samalla suurin alaraja 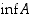 .
.
Opiskeluvideo: S2: Joukon supremum ja infimum 
