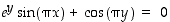Harjoitustehtäviä

170.   Tarkastellaan yhtälön 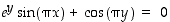määräämää derivoituvaa tasokäyrää.

(a) Piste 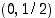on eräs käyrän piste. Etsi käyrältä neljä muuta tarkasti määrättyä (ei likiarvoista) pistettä, yksi kustakin tason neljänneksestä (ja koordinaattiakselien ulkopuolelta).

(b) Valitse yksi käyrän piste ja määrää ratkaisukäyrän tangentin yhtälö siinä pisteessä.

(c) Osoita, että funktiolla 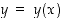on valitsemasi pisteen ympäristössä käänteisfunktio ja määrää käänteisfunktion derivaatta tämän valitsemasi pisteen kuvapisteessä.

171.   Millä vakioiden 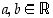arvoilla funktio 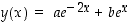toteuttaa ns. differentiaaliyhtälön ?

172.   Määrää .

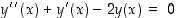173.   Montako positiivista ratkaisua on yhtälöllä 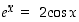? Ratkaise yksi likimääräisesti (vähintään 5 desimaalia).

174.   Millä muuttujan 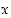arvoilla funktio 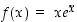on aidosti kasvava? Määritä lisäksi 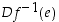(rajaamalla tarvittaessa funktio sellaiselle välille, jossa käänteisfunktio on olemassa).

175.   Osoita, että yhtälöllä 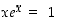on täsmälleen yksi ratkaisu. Ratkaise se likimääräisesti (vähintään 5 desimaalia).

176.   Määrää funktion 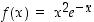ääriarvot, käännepisteet ja asymptootit. Hahmottele kuvaajaa.

177.   Määritä