Käännepiste
Piste 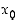 on funktion
on funktion 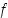 käännepiste tai käännekohta, jos toinen derivaatta on olemassa pisteen
käännepiste tai käännekohta, jos toinen derivaatta on olemassa pisteen 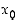 ympäristössä ja jos toinen derivaatta muuttaa merkkiään pisteen
ympäristössä ja jos toinen derivaatta muuttaa merkkiään pisteen 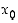 kohdalla. Toista derivaattaa ei kuitenkaan tarvitse olla olemassa pisteessä
kohdalla. Toista derivaattaa ei kuitenkaan tarvitse olla olemassa pisteessä 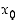 . Käännepisteen kohdalla funktion kuperuus muuttuu ylöspäin kuperasta alaspäin kuperaksi (kun toinen derivaatta muuttuu negatiivisesta positiiviseksi) tai päinvastoin.
. Käännepisteen kohdalla funktion kuperuus muuttuu ylöspäin kuperasta alaspäin kuperaksi (kun toinen derivaatta muuttuu negatiivisesta positiiviseksi) tai päinvastoin.
Esimerkki 5.3.6.
Sinifunktiolle 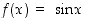 toinen derivaatta
toinen derivaatta 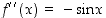 on nolla pisteissä
on nolla pisteissä 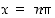 ja jokaisessa näistä toinen derivaatta muuttaa merkkiään. Ne ovat siis kaikki funktion
ja jokaisessa näistä toinen derivaatta muuttaa merkkiään. Ne ovat siis kaikki funktion 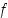 käännepisteitä (joista kolme on merkitty kuvaan 48).
käännepisteitä (joista kolme on merkitty kuvaan 48).
Kuva 48.

Esimerkki 5.3.7.
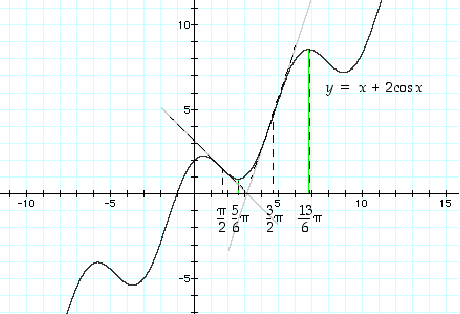
Selvitetään funktion 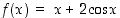 käyttäytymistä. Tämä funktio on kaikkialla (ainakin) kahdesti derivoituva. Derivaatta
käyttäytymistä. Tämä funktio on kaikkialla (ainakin) kahdesti derivoituva. Derivaatta 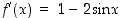 on nolla, kun
on nolla, kun 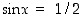 eli kun
eli kun 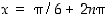 tai
tai 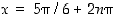 . Edelleen toinen derivaatta on
. Edelleen toinen derivaatta on 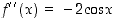 . Kohdissa
. Kohdissa 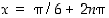 on
on 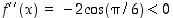 ,
joten nämä kohdat ovat paikallisia maksimikohtia. Kohdissa
,
joten nämä kohdat ovat paikallisia maksimikohtia. Kohdissa 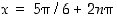 on taas
on taas 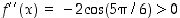 ,
joten nämä kohdat ovat vuorostaan paikallisia minimikohtia.
,
joten nämä kohdat ovat vuorostaan paikallisia minimikohtia.
Toisen derivaatan nollakohdat 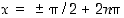 ovat sen käännepisteitä, sillä näissä kohdissa myös toisen derivaatan merkki vaihtuu. Katso kuva 49.
ovat sen käännepisteitä, sillä näissä kohdissa myös toisen derivaatan merkki vaihtuu. Katso kuva 49.
Kuva 49.

Opiskeluvideo: K3: Funktion käännepisteet ja kuperuus 

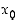 on funktion
on funktion 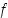 käännepiste tai käännekohta, jos toinen derivaatta on olemassa pisteen
käännepiste tai käännekohta, jos toinen derivaatta on olemassa pisteen 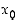 ympäristössä ja jos toinen derivaatta muuttaa merkkiään pisteen
ympäristössä ja jos toinen derivaatta muuttaa merkkiään pisteen 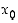 kohdalla. Toista derivaattaa ei kuitenkaan tarvitse olla olemassa pisteessä
kohdalla. Toista derivaattaa ei kuitenkaan tarvitse olla olemassa pisteessä 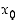 . Käännepisteen kohdalla funktion kuperuus muuttuu ylöspäin kuperasta alaspäin kuperaksi (kun toinen derivaatta muuttuu negatiivisesta positiiviseksi) tai päinvastoin.
. Käännepisteen kohdalla funktion kuperuus muuttuu ylöspäin kuperasta alaspäin kuperaksi (kun toinen derivaatta muuttuu negatiivisesta positiiviseksi) tai päinvastoin. 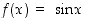 toinen derivaatta
toinen derivaatta 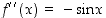 on nolla pisteissä
on nolla pisteissä 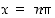 ja jokaisessa näistä toinen derivaatta muuttaa merkkiään. Ne ovat siis kaikki funktion
ja jokaisessa näistä toinen derivaatta muuttaa merkkiään. Ne ovat siis kaikki funktion 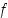 käännepisteitä (joista kolme on merkitty kuvaan
käännepisteitä (joista kolme on merkitty kuvaan 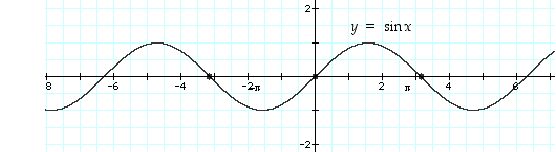

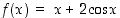 käyttäytymistä. Tämä funktio on kaikkialla (ainakin) kahdesti derivoituva. Derivaatta
käyttäytymistä. Tämä funktio on kaikkialla (ainakin) kahdesti derivoituva. Derivaatta 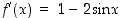 on nolla, kun
on nolla, kun 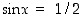 eli kun
eli kun 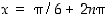 tai
tai 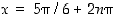 . Edelleen toinen derivaatta on
. Edelleen toinen derivaatta on 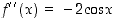 . Kohdissa
. Kohdissa 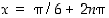 on
on 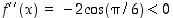 ,
joten nämä kohdat ovat paikallisia maksimikohtia. Kohdissa
,
joten nämä kohdat ovat paikallisia maksimikohtia. Kohdissa 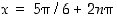 on taas
on taas 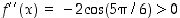 ,
joten nämä kohdat ovat vuorostaan paikallisia minimikohtia.
,
joten nämä kohdat ovat vuorostaan paikallisia minimikohtia. 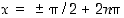 ovat sen käännepisteitä, sillä näissä kohdissa myös toisen derivaatan merkki vaihtuu. Katso kuva
ovat sen käännepisteitä, sillä näissä kohdissa myös toisen derivaatan merkki vaihtuu. Katso kuva