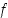 sanotaan olevan alaspäin kupera välillä
sanotaan olevan alaspäin kupera välillä 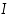 ,
jos sen kuvaaja on jokaisen välillä
,
jos sen kuvaaja on jokaisen välillä 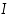 piirretyn tangenttinsa yläpuolella sivuamispistettä lukuunottamatta. Derivoituva funktio
piirretyn tangenttinsa yläpuolella sivuamispistettä lukuunottamatta. Derivoituva funktio 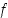 on siten alaspäin kupera, jos
on siten alaspäin kupera, jos
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tutkitaan derivoituvan funktion kuvaajaa geometrisesti. Funktion 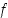 sanotaan olevan alaspäin kupera välillä
sanotaan olevan alaspäin kupera välillä 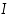 ,
jos sen kuvaaja on jokaisen välillä
,
jos sen kuvaaja on jokaisen välillä 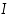 piirretyn tangenttinsa yläpuolella sivuamispistettä lukuunottamatta. Derivoituva funktio
piirretyn tangenttinsa yläpuolella sivuamispistettä lukuunottamatta. Derivoituva funktio 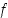 on siten alaspäin kupera, jos
on siten alaspäin kupera, jos

Vastaavasti derivoituva funktio 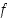 on ylöspäin kupera, jos sen kuvaaja on jokaisen välillä
on ylöspäin kupera, jos sen kuvaaja on jokaisen välillä 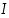 piirretyn tangenttinsa alapuolella sivuamispistettä lukuunottamatta. Funktio f on täten ylöspäin kupera, jos
piirretyn tangenttinsa alapuolella sivuamispistettä lukuunottamatta. Funktio f on täten ylöspäin kupera, jos
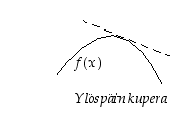
Koska 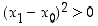 ,
kun
,
kun 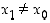 ,
on funktio
,
on funktio 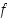 alaspäin kupera koko reaalialueella.
alaspäin kupera koko reaalialueella.
Määritelmää helpommin kuperuutta voidaan usein selvittää derivaatan kasvavuuden tai toisen derivaatan merkin avulla.
Lause 5.3.2. (1. kuperuustesti)
Olkoon 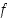 välillä
välillä  määritelty jatkuva funktio, joka on derivoituva välin sisäpisteissä.
määritelty jatkuva funktio, joka on derivoituva välin sisäpisteissä.
(a) Jos derivaatta 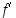 on aidosti kasvava välin
on aidosti kasvava välin 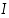 sisäpisteissä, funktio
sisäpisteissä, funktio 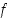 on alaspäin kupera.
on alaspäin kupera.
(b) Jos derivaatta 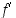 on aidosti vähenevä välin
on aidosti vähenevä välin 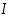 sisäpisteissä, funktio
sisäpisteissä, funktio 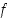 on ylöspäin kupera.
on ylöspäin kupera.
Todistus. Olkoon 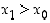 . Differentiaalilaskennan väliarvolauseen mukaan on
. Differentiaalilaskennan väliarvolauseen mukaan on
jollekin pisteelle 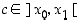 . Jos
. Jos 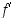 on aidosti kasvava, on
on aidosti kasvava, on 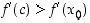 ja siten
ja siten
Tästä nähdään funktion 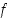 alaspäin kuperuus välillä
alaspäin kuperuus välillä 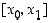 . Vastaavasti käsitellään aidosti vähenevä tapaus.
. Vastaavasti käsitellään aidosti vähenevä tapaus.
Lause 5.3.3. (2. kuperuustesti)
Olkoon 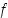 välillä
välillä 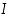 määritelty jatkuva funktio, joka on kahdesti derivoituva välin sisäpisteissä.
määritelty jatkuva funktio, joka on kahdesti derivoituva välin sisäpisteissä.
(a) Jos 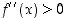 välin
välin 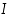 sisäpisteissä, funktio
sisäpisteissä, funktio 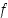 on alaspäin kupera.
on alaspäin kupera.
(b) Jos 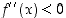 välin
välin 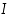 sisäpisteissä, funktio
sisäpisteissä, funktio  on ylöspäin kupera.
on ylöspäin kupera.
Todistus. Toisen derivaatan positiivisuudesta (negatiivisuudesta) seuraa ensimmäisen derivaatan aito kasvavuus (vast. vähenevyys), joten väitteet seuraavat tämän jälkeen edellisestä lauseesta.
Funktion 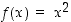 derivaatta
derivaatta 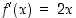 on aidosti kasvava, joten
on aidosti kasvava, joten  on alaspäin kupera.
on alaspäin kupera.
Sinifunktiolle 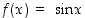 toinen derivaatta
toinen derivaatta 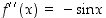 on positiivinen, kun
on positiivinen, kun 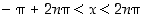 ,
ja negatiivinen, kun
,
ja negatiivinen, kun 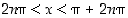 . Sinifunktio on siten alaspäin kupera väleillä
. Sinifunktio on siten alaspäin kupera väleillä 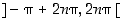 ja ylöspäin kupera väleillä
ja ylöspäin kupera väleillä 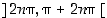 . Katso kuvaa 48.
. Katso kuvaa 48.