Yhteenveto ääriarvojen etsinnästä:
(1) Selvitä funktion määrittelyjoukko, ellei sitä ole annettu.
(2) Selvitä mahdolliset epäjatkuvuuspisteet.
(3) Selvitä mahdolliset epäderivoituvuuspisteet.
(4) Selvitä mahdolliset derivaatan nollakohdat.
(5) Huomioi mahdolliset määrittelyvälin (tai -välien) päätepisteet.
(6) Kunkin edellä saadun ehdokaspisteen kohdalla selvitä, onko se paikallinen tai globaali ääriarvokohta.
Esimerkki 5.1.6.
Tutkitaan funktion 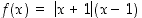 ääriarvoja. Funktio
ääriarvoja. Funktio 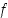 on jatkuva kahden jatkuvan funktion tulona. Lisäksi se on derivoituva ainakin, kun
on jatkuva kahden jatkuvan funktion tulona. Lisäksi se on derivoituva ainakin, kun 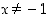 (pisteessä
(pisteessä 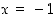 lausekkeessa oleva itseisarvofunktio ei ole derivoituva). Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan välttämättä selvittää derivoituvuutta pisteessä
lausekkeessa oleva itseisarvofunktio ei ole derivoituva). Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan välttämättä selvittää derivoituvuutta pisteessä 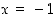 . Riittää, että tämä piste huomioidaan yhtenä ehdokkaana ääriarvokohdaksi.
. Riittää, että tämä piste huomioidaan yhtenä ehdokkaana ääriarvokohdaksi.
Selvitetään funktion  derivaatan nollakohdat. Koska
derivaatan nollakohdat. Koska
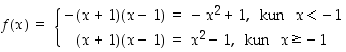
on
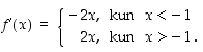
Siten piste 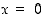 on ainoa derivaatan nollakohta.
on ainoa derivaatan nollakohta.
On saatu kaksi ehdokasta ääriarvokohdiksi. Derivaatan merkin perusteella saadaan seuraava taulukko (esimerkiksi 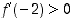 ,
,
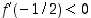 ja
ja 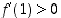 ).
).
Taulukosta nähdään, että piste 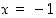 on paikallinen maksimikohta ja piste
on paikallinen maksimikohta ja piste 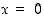 on paikallinen minimikohta. Näissä kohdissa vastaavat paikalliset ääriarvot ovat
on paikallinen minimikohta. Näissä kohdissa vastaavat paikalliset ääriarvot ovat 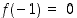 ja
ja 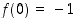 .
.
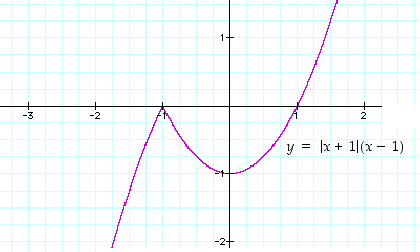
Huomaa, että funktio 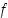 ei saa suurinta eikä pienintä arvoa, sillä
ei saa suurinta eikä pienintä arvoa, sillä 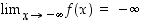 ja
ja 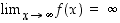 . Katso kuva 44.
. Katso kuva 44.
Kuva 44. Esimerkin 5.1.6 kuva

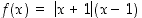 ääriarvoja. Funktio
ääriarvoja. Funktio 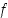 on jatkuva kahden jatkuvan funktion tulona. Lisäksi se on derivoituva ainakin, kun
on jatkuva kahden jatkuvan funktion tulona. Lisäksi se on derivoituva ainakin, kun 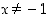 (pisteessä
(pisteessä 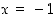 lausekkeessa oleva itseisarvofunktio ei ole derivoituva). Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan välttämättä selvittää derivoituvuutta pisteessä
lausekkeessa oleva itseisarvofunktio ei ole derivoituva). Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan välttämättä selvittää derivoituvuutta pisteessä 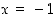 . Riittää, että tämä piste huomioidaan yhtenä ehdokkaana ääriarvokohdaksi.
. Riittää, että tämä piste huomioidaan yhtenä ehdokkaana ääriarvokohdaksi. 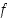 derivaatan nollakohdat. Koska
derivaatan nollakohdat. Koska 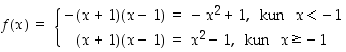
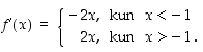
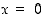 on ainoa derivaatan nollakohta.
on ainoa derivaatan nollakohta. 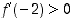 ,
,
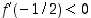 ja
ja 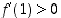 ).
). 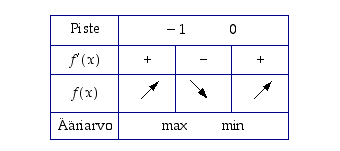
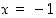 on paikallinen maksimikohta ja piste
on paikallinen maksimikohta ja piste 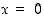 on paikallinen minimikohta. Näissä kohdissa vastaavat paikalliset ääriarvot ovat
on paikallinen minimikohta. Näissä kohdissa vastaavat paikalliset ääriarvot ovat 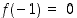 ja
ja 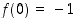 .
.  ei saa suurinta eikä pienintä arvoa, sillä
ei saa suurinta eikä pienintä arvoa, sillä 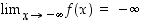 ja
ja 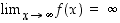 . Katso kuva
. Katso kuva