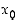 on funktion
on funktion 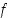 paikallinen ääriarvokohta ja jos
paikallinen ääriarvokohta ja jos 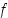 on derivoituva pisteessä
on derivoituva pisteessä 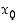 ,
on
,
on 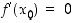 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Derivoituvalle funktiolle voidaan derivaatan avulla tutkia, onko jokin piste mahdollisesti paikallinen ääriarvokohta.
Jos piste 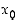 on funktion
on funktion 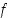 paikallinen ääriarvokohta ja jos
paikallinen ääriarvokohta ja jos 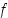 on derivoituva pisteessä
on derivoituva pisteessä 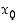 ,
on
,
on 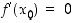 .
.
Todistus. Olkoon väli  sellainen pisteen
sellainen pisteen 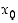 sisältävä väli, että funktio
sisältävä väli, että funktio 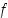 saa sillä välillä globaalin ääriarvon kohdassa
saa sillä välillä globaalin ääriarvon kohdassa 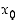 . Tämän jälkeen väite todistetaan kuten Rollen lauseessa (lause 4.1.1).
. Tämän jälkeen väite todistetaan kuten Rollen lauseessa (lause 4.1.1).
Edellisen lauseen ehto 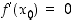 ei ole kuitenkaan riittävä ehto sille, että piste
ei ole kuitenkaan riittävä ehto sille, että piste 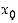 olisi paikallinen ääriarvo. Se antaa vain ehdokkaan paikalliseksi ääriarvokohdaksi.
olisi paikallinen ääriarvo. Se antaa vain ehdokkaan paikalliseksi ääriarvokohdaksi.
Funktiolle 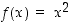 on
on 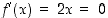 ,
kun
,
kun 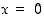 . Siten nolla on ehdokas paikalliseksi ääriarvokohdaksi. Koska
. Siten nolla on ehdokas paikalliseksi ääriarvokohdaksi. Koska 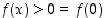 ,
kun
,
kun 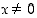 ,
on nolla paikallinen minimikohta ja samalla globaali minimikohta (ja nolla on funktion pienin arvo).
,
on nolla paikallinen minimikohta ja samalla globaali minimikohta (ja nolla on funktion pienin arvo).
Funktiolle 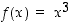 on
on 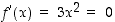 ,
kun
,
kun 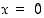 . Siten nytkin nolla on ehdokas paikalliseksi ääriarvokohdaksi. Koska
. Siten nytkin nolla on ehdokas paikalliseksi ääriarvokohdaksi. Koska 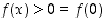 ,
kun
,
kun 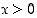 ja
ja 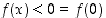 ,
kun
,
kun 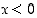 ,
ei nolla ole kuitenkaan paikallinen ääriarvokohta.
,
ei nolla ole kuitenkaan paikallinen ääriarvokohta.
Funktio 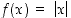 ei ole derivoituva nollassa, mutta silti nolla on sen paikallinen minimikohta ja samalla globaali minimikohta. Paikallisessa ääriarvokohdassa ei siis välttämättä tarvitse derivaattaa olla olemassakaan.
ei ole derivoituva nollassa, mutta silti nolla on sen paikallinen minimikohta ja samalla globaali minimikohta. Paikallisessa ääriarvokohdassa ei siis välttämättä tarvitse derivaattaa olla olemassakaan.
Jos funktio on derivoituva derivaatan nollakohdan ympäristössäkin, voidaan ääriarvon laatu selvittää derivaatan merkistä.
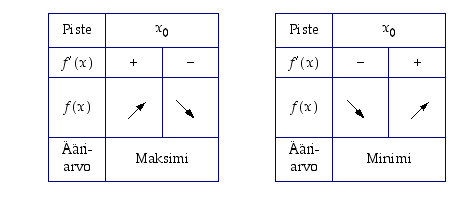
Lause 5.1.5. (1. ääriarvotesti)
Olkoon funktio 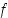 jatkuva pisteessä
jatkuva pisteessä 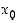 ja derivoituva pisteen
ja derivoituva pisteen 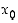 sisältävällä avoimella välillä
sisältävällä avoimella välillä 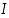 ,
paitsi mahdollisesti pisteessä
,
paitsi mahdollisesti pisteessä 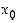 . Jos derivaatta
. Jos derivaatta 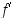 on erimerkkinen pisteen
on erimerkkinen pisteen 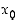 eri puolilla, on piste
eri puolilla, on piste 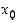 funktion
funktion 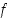 paikallinen ääriarvokohta.
paikallinen ääriarvokohta.
Todistus. Olkoon esimerkiksi 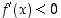 ,
kun
,
kun 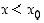 ,
ja
,
ja 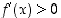 ,
kun
,
kun 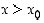 . Tällöin derivaatan monotonisuustestin perusteella
. Tällöin derivaatan monotonisuustestin perusteella 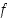 on aidosti kasvava pisteen
on aidosti kasvava pisteen 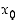 vasemmalla puolella ja aidosti vähenevä pisteen
vasemmalla puolella ja aidosti vähenevä pisteen 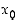 oikealla puolella (piste
oikealla puolella (piste 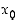 kummassakin tapauksessa mukaan lukien). Niinpä
kummassakin tapauksessa mukaan lukien). Niinpä 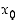 on paikallinen maksimikohta.
on paikallinen maksimikohta.
Vastaavasti selvitetään tilanne, jossa derivaatan merkki muuttuu positiivisesta negatiiviseksi. Tällöin 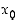 on paikallinen minimikohta.
on paikallinen minimikohta.
Huomaa edellä olevan lauseen muotoilussa, että funktiolla 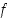 ei tarvitse olla derivaattaa itse tarkastelupisteessä
ei tarvitse olla derivaattaa itse tarkastelupisteessä 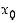 ,
mutta funktion pitää kylläkin olla jatkuva siinä pisteessä. Lauseen tilannetta kuvaavat seuraavat taulukot.
,
mutta funktion pitää kylläkin olla jatkuva siinä pisteessä. Lauseen tilannetta kuvaavat seuraavat taulukot.
Opiskelutehtävä 27. (Derivoituvan funktion kuvaaja)
Piirrä sellaisen kaikilla reaaliluvuilla määritellyn funktion 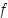 kuvaaja, joka toteuttaa kaikki seuraavat ehdot
kuvaaja, joka toteuttaa kaikki seuraavat ehdot
(a) 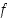 on derivoituva pisteessä
on derivoituva pisteessä 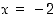 ,
joka on funktion
,
joka on funktion 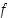 lokaali minimikohta,
lokaali minimikohta,
(b) 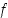 on jatkuva, mutta ei derivoituva pisteessä
on jatkuva, mutta ei derivoituva pisteessä 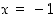 ,
joka on funktion
,
joka on funktion 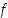 lokaali maksimikohta,
lokaali maksimikohta,
(c) 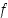 :n derivaatta pisteessä
:n derivaatta pisteessä 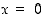 on nolla, mutta piste
on nolla, mutta piste 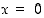 ei ole funktion
ei ole funktion 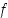 ääriarvokohta,
ääriarvokohta,
(d) 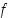 on epäjatkuva pisteessä
on epäjatkuva pisteessä 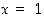 ,
joka on
,
joka on 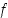 :n lokaali minimikohta,
:n lokaali minimikohta,
(e) 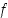 on jatkuva, mutta ei derivoituva pisteessä
on jatkuva, mutta ei derivoituva pisteessä 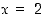 ,
joka ei ole funktion
,
joka ei ole funktion 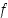 lokaali ääriarvokohta,
lokaali ääriarvokohta,
(f) 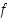 on epäjatkuva pisteessä
on epäjatkuva pisteessä 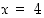 ,
joka ei ole
,
joka ei ole 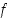 :n lokaali ääriarvokohta.
:n lokaali ääriarvokohta.
Opiskeluvideo: K1: Funktion ääriarvot 
