Ääriarvot ja paikalliset ääriarvot
Funktio 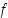 saa suurimman arvonsa tai maksimiarvonsa pisteessä
saa suurimman arvonsa tai maksimiarvonsa pisteessä 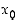 ,
jos arvo
,
jos arvo 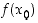 on kaikista funktion saamista arvoista suurin ts. jos
on kaikista funktion saamista arvoista suurin ts. jos 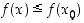 kaikilla
kaikilla 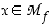 . Vastaavasti funktio
. Vastaavasti funktio 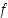 saa pienimmän arvonsa tai minimiarvonsa pisteessä
saa pienimmän arvonsa tai minimiarvonsa pisteessä 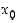 ,
jos arvo
,
jos arvo 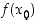 on kaikista funktion saamista arvoista pienin. Suurin ja pienin arvo muodostavat funktion ääriarvot, ja ne kohdat
on kaikista funktion saamista arvoista pienin. Suurin ja pienin arvo muodostavat funktion ääriarvot, ja ne kohdat 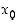 ,
joissa nämä arvot saavutetaan, ovat funktion ääriarvokohdat.
,
joissa nämä arvot saavutetaan, ovat funktion ääriarvokohdat.
Funktio ei välttämättä saa suurinta tai pienintä arvoaan. Esimerkiksi funktiolla 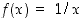 ei ole suurinta eikä pienintä arvoa, ei edes positiivisille luvuille rajoitettuna. Funktio
ei ole suurinta eikä pienintä arvoa, ei edes positiivisille luvuille rajoitettuna. Funktio
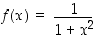
taas saa suurimman arvonsa 1 pisteessä 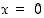 ,
mutta sillä ei ole pienintä arvoa. Funktio
,
mutta sillä ei ole pienintä arvoa. Funktio 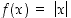 vuorostaan saa pienimmän arvonsa 0 pisteessä
vuorostaan saa pienimmän arvonsa 0 pisteessä 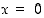 ,
mutta sillä ei ole suurinta arvoa.
,
mutta sillä ei ole suurinta arvoa.
Jos funktio on jatkuva suljetulla välillä, se saa Weierstrassin lauseen mukaan sillä välillä suurimman ja pienimmän arvonsa. Lause ei kuitenkaan anna käytännön keinoa näitten ääriarvojen määräämiseen. Epäjatkuva funktio voi esimerkiksi saada ääriarvonsa epäjatkuvuuspisteissä. Derivoituvalle funktiolle voidaan kuitenkin mahdollisia ääriarvokohtia etsiä derivaatan avulla.
Yleistämme ääriarvokäsitteen rajoittumafunktioille eli tilanteesen, jossa funktion tarkastelu rajataan jollekin määrittelyjoukon osavälille.
Piste 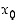 on funktion
on funktion 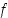 paikallinen maksimikohta, jos on olemassa jokin pisteen
paikallinen maksimikohta, jos on olemassa jokin pisteen 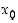 sisältävä avoin väli
sisältävä avoin väli 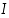 ,
jolla arvo
,
jolla arvo 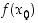 on suurin funktion
on suurin funktion 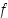 saama arvo ts.
saama arvo ts. 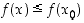 kaikilla
kaikilla 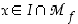 . Arvo
. Arvo 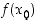 on tällöin paikallinen maksimi. Vastaavasti piste
on tällöin paikallinen maksimi. Vastaavasti piste 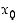 on funktion
on funktion 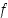 paikallinen minimikohta, jos on olemassa sellainen pisteen
paikallinen minimikohta, jos on olemassa sellainen pisteen 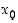 sisältävä avoin väli
sisältävä avoin väli 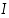 ,
jolla arvo
,
jolla arvo 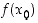 on pienin funktion
on pienin funktion 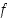 saama arvo ts.
saama arvo ts. 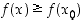 kaikilla
kaikilla 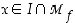 . Arvo
. Arvo 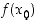 on tällöin paikallinen minimi. Paikalliset maksimi- ja minimikohdat ovat yhteisnimitykseltään paikallisia eli lokaaleja ääriarvokohtia ja niitä vastaavat funktion arvot paikallisia eli lokaaleja ääriarvoja. Huomaa, että paikallinen ääriarvokohta voi olla myös suljetun välin reunapiste, mikäli funktiota ei ole määritelty reunapisteen toisella puolella. Ääritapauksessa ääriarvokohta voi olla määrittelyjoukon erillinen piste.
on tällöin paikallinen minimi. Paikalliset maksimi- ja minimikohdat ovat yhteisnimitykseltään paikallisia eli lokaaleja ääriarvokohtia ja niitä vastaavat funktion arvot paikallisia eli lokaaleja ääriarvoja. Huomaa, että paikallinen ääriarvokohta voi olla myös suljetun välin reunapiste, mikäli funktiota ei ole määritelty reunapisteen toisella puolella. Ääritapauksessa ääriarvokohta voi olla määrittelyjoukon erillinen piste.
Paikallisen ääriarvon ei tarvitse olla funktion suurin tai pienin arvo, mutta suurin ja pienin arvo ovat aina myös paikallisia ääriarvoja. Funktion suurinta ja pienintä arvoa sanotaan myös globaaleiksi ääriarvoiksi. Funktiolla on siten paikallinen ääriarvokohta jossain pisteessä, jos se on jollakin tämän pisteen sisältävällä välillä rajoittumafunktion globaali ääriarvokohta.
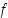 saa suurimman arvonsa tai maksimiarvonsa pisteessä
saa suurimman arvonsa tai maksimiarvonsa pisteessä 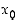 ,
jos arvo
,
jos arvo 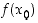 on kaikista funktion saamista arvoista suurin ts. jos
on kaikista funktion saamista arvoista suurin ts. jos 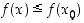 kaikilla
kaikilla 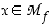 . Vastaavasti funktio
. Vastaavasti funktio 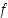 saa pienimmän arvonsa tai minimiarvonsa pisteessä
saa pienimmän arvonsa tai minimiarvonsa pisteessä 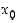 ,
jos arvo
,
jos arvo 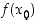 on kaikista funktion saamista arvoista pienin. Suurin ja pienin arvo muodostavat funktion ääriarvot, ja ne kohdat
on kaikista funktion saamista arvoista pienin. Suurin ja pienin arvo muodostavat funktion ääriarvot, ja ne kohdat 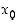 ,
joissa nämä arvot saavutetaan, ovat funktion ääriarvokohdat.
,
joissa nämä arvot saavutetaan, ovat funktion ääriarvokohdat. 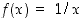 ei ole suurinta eikä pienintä arvoa, ei edes positiivisille luvuille rajoitettuna. Funktio
ei ole suurinta eikä pienintä arvoa, ei edes positiivisille luvuille rajoitettuna. Funktio 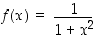
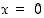 ,
mutta sillä ei ole pienintä arvoa. Funktio
,
mutta sillä ei ole pienintä arvoa. Funktio 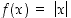 vuorostaan saa pienimmän arvonsa 0 pisteessä
vuorostaan saa pienimmän arvonsa 0 pisteessä 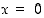 ,
mutta sillä ei ole suurinta arvoa.
,
mutta sillä ei ole suurinta arvoa. 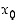 on funktion
on funktion 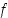 paikallinen
paikallinen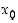 sisältävä avoin väli
sisältävä avoin väli 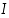 ,
jolla arvo
,
jolla arvo 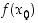 on suurin funktion
on suurin funktion 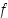 saama arvo ts.
saama arvo ts. 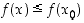 kaikilla
kaikilla 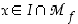 . Arvo
. Arvo 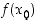 on tällöin paikallinen maksimi
on tällöin paikallinen maksimi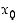 on funktion
on funktion 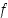 paikallinen minimikohta
paikallinen minimikohta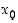 sisältävä avoin väli
sisältävä avoin väli 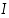 ,
jolla arvo
,
jolla arvo 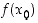 on pienin funktion
on pienin funktion 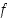 saama arvo ts.
saama arvo ts. 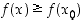 kaikilla
kaikilla 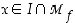 . Arvo
. Arvo 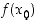 on tällöin paikallinen minimi
on tällöin paikallinen minimi