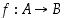 on käänteisfunktio
on käänteisfunktio 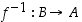 ja sen määrittelee ehto
ja sen määrittelee ehto
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tiedämme, että bijektiolla 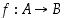 on käänteisfunktio
on käänteisfunktio 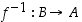 ja sen määrittelee ehto
ja sen määrittelee ehto
Esimerkiksi funktiolle 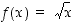 ,
kun
,
kun 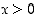 ,
yhtälöstä
,
yhtälöstä 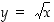 saadaan ratkaisuksi
saadaan ratkaisuksi 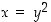 ,
joten käänteisfunktio on
,
joten käänteisfunktio on 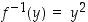 ,
kun
,
kun 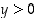 . Yleensä käänteisfunktion argumentiksi vaihdetaan myös
. Yleensä käänteisfunktion argumentiksi vaihdetaan myös 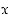 . Tämän mukaan edellä on
. Tämän mukaan edellä on 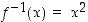 ,
kun
,
kun 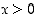 .
.
Kun tarkastellaan funktion ja sen käänteisfunktion kuvaajia eli käyriä 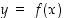 ja
ja 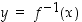 ,
huomataan, että ne ovat toistensa peilikuvia suoran
,
huomataan, että ne ovat toistensa peilikuvia suoran 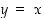 suhteen, ts. jos piste
suhteen, ts. jos piste 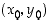 on funktion
on funktion 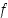 kuvaajalla, on piste
kuvaajalla, on piste 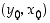 käänteisfunktion
käänteisfunktion 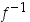 kuvaajalla. Katso kuva 41.
kuvaajalla. Katso kuva 41.
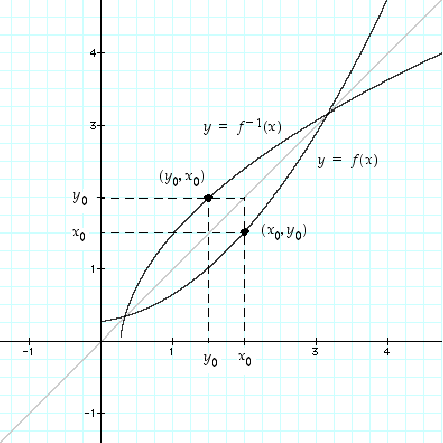
On selvää, että jatkuvan funktion on oltava monotoninen, jotta sillä olisi käänteisfunktio. Toisaalta pätee seuraava.
Aidosti monotoninen funktio on bijektio lähtöjoukoltaan arvojoukolleen.
Todistus. Jos funktio 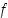 on aidosti monotoninen, eri pisteiden kuvat ovat aina eri suuria. Siten
on aidosti monotoninen, eri pisteiden kuvat ovat aina eri suuria. Siten 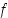 on injektio. Surjektiivisuus seuraa maalijoukon rajaamisesta arvojoukoksi.
on injektio. Surjektiivisuus seuraa maalijoukon rajaamisesta arvojoukoksi.
Jos funktio on monotonisuuden lisäksi jatkuva tai peräti derivoituva, voidaan käänteisfunktiosta sanoa enemmän. Tätä käsittelevät seuraavat kaksi tulosta.
Lause 4.4.2. (Käänteiskuvauksen jatkuvuus)
Välillä  määritellylle aidosti monotoniselle jatkuvalle funktiolle on kuvajoukko
määritellylle aidosti monotoniselle jatkuvalle funktiolle on kuvajoukko 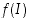 myös väli ja käänteiskuvaus
myös väli ja käänteiskuvaus 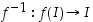 on aidosti monotoninen ja jatkuva (aidosti kasvavan käänteiskuvaus on aidosti kasvava ja aidosti vähenevän käänteiskuvaus on aidosti vähenevä).
on aidosti monotoninen ja jatkuva (aidosti kasvavan käänteiskuvaus on aidosti kasvava ja aidosti vähenevän käänteiskuvaus on aidosti vähenevä).
Todistus. Olkoon 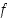 aidosti kasvava (aidosti vähenevälle todistus tehdään vastaavasti). Osoitetaan aluksi, että
aidosti kasvava (aidosti vähenevälle todistus tehdään vastaavasti). Osoitetaan aluksi, että 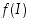 on myös väli. Olkoot
on myös väli. Olkoot 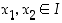 ja
ja 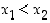 . Silloin
. Silloin 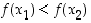 . Jos nyt
. Jos nyt 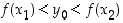 ,
on jatkuvien funktioiden väliarvolauseen mukaan
,
on jatkuvien funktioiden väliarvolauseen mukaan 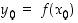 jollekin
jollekin 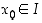 . Siispä
. Siispä 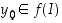 . Täten
. Täten 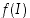 sisältää kaikkien pisteidensä lisäksi kaikki niiden välipisteetkin eli se on itsekin väli.
sisältää kaikkien pisteidensä lisäksi kaikki niiden välipisteetkin eli se on itsekin väli.
Edellisen lauseen 4.4.1 mukaan on olemassa käänteiskuvaus 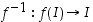 . Osoitetaan se ensin aidosti kasvavaksi. Oletetaan, että näin ei olisi, vaan että olisi olemassa
. Osoitetaan se ensin aidosti kasvavaksi. Oletetaan, että näin ei olisi, vaan että olisi olemassa 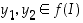 ,
joille
,
joille 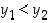 ja
ja 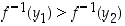 . Tällöin funktion
. Tällöin funktion 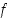 aidon kasvavuuden perusteella olisi
aidon kasvavuuden perusteella olisi
eli 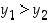 . Mutta tämähän on ristiriita edellä olevan kanssa. Funktio
. Mutta tämähän on ristiriita edellä olevan kanssa. Funktio 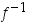 on siten aidosti kasvava.
on siten aidosti kasvava.
Osoitetaan vielä funktion 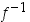 jatkuvuus. Katso sitä varten kuvaa 42.
jatkuvuus. Katso sitä varten kuvaa 42.
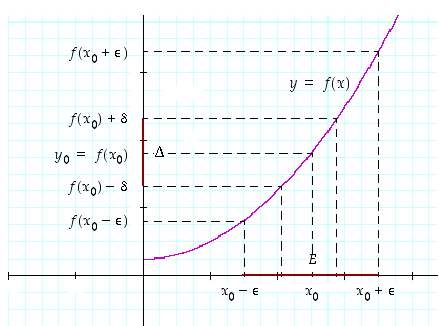
Olkoon 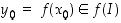 ja luku
ja luku 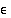 niin pieni, että väli
niin pieni, että väli 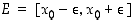 kuuluu väliin
kuuluu väliin 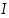 . Funktion
. Funktion 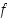 aidon kasvavuuden perusteella on
aidon kasvavuuden perusteella on 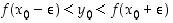 . Siten on olemassa väli
. Siten on olemassa väli 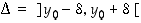 ,
joka sisältyy väliin
,
joka sisältyy väliin 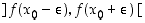 . Lisäksi funktion
. Lisäksi funktion 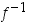 edellä todistetun aidon kasvavuuden perusteella on
edellä todistetun aidon kasvavuuden perusteella on 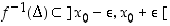 . Funktion
. Funktion 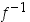 on siten jatkuva.
on siten jatkuva.
Opiskeluvideo: D9: Käänteisfunktion olemassaolo 
