Harjoitustehtäviä
146. Tarkastellaan funktiota 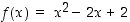 välillä
välillä 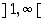 ja rajoitetaan maalijoukko niin, että funktio on surjektio. Mikä on silloin maalijoukko? Osoita, että tällä funktiolla
ja rajoitetaan maalijoukko niin, että funktio on surjektio. Mikä on silloin maalijoukko? Osoita, että tällä funktiolla 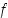 on olemassa käänteisfunktio. Mikä on sen lauseke? Laske edelleen käänteisfunktion derivaatta pisteessä
on olemassa käänteisfunktio. Mikä on sen lauseke? Laske edelleen käänteisfunktion derivaatta pisteessä 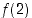 sekä derivoimalla saatu lauseke että ratkaisemalla se funktion
sekä derivoimalla saatu lauseke että ratkaisemalla se funktion 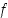 derivaatan avulla.
derivaatan avulla.
147. Määrää käänteisfunktion derivoimissäännön avulla funktion 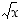 derivaatta.
derivaatta.
148. Näytä, että funktio 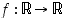 ,
,
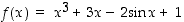 on bijektio. Laske edelleen käänteisfunktion derivaatta jossain valitsemassasi pisteessä.
on bijektio. Laske edelleen käänteisfunktion derivaatta jossain valitsemassasi pisteessä.
149. Osoita, että funktiolla
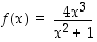
on käänteisfunktio ja määrää käänteisfunktion derivaatta jossain pisteessä.
150. Määrää laajin pisteen 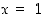 sisältävä väli, jolla funktiolla
sisältävä väli, jolla funktiolla 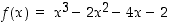 on käänteisfunktio. Määrää käänteisfunktion derivaatta pisteessä
on käänteisfunktio. Määrää käänteisfunktion derivaatta pisteessä 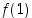 .
.
151. (a) Perustele, miksi funktiolla 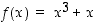 on kaikkialla määritelty käänteisfunktio.
on kaikkialla määritelty käänteisfunktio.
(b) Missä pisteissä 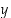 on voimassa epäyhtälö
on voimassa epäyhtälö 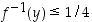 ?
?
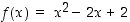 välillä
välillä 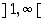 ja rajoitetaan maalijoukko niin, että funktio on surjektio. Mikä on silloin maalijoukko? Osoita, että tällä funktiolla
ja rajoitetaan maalijoukko niin, että funktio on surjektio. Mikä on silloin maalijoukko? Osoita, että tällä funktiolla 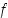 on olemassa käänteisfunktio. Mikä on sen lauseke? Laske edelleen käänteisfunktion derivaatta pisteessä
on olemassa käänteisfunktio. Mikä on sen lauseke? Laske edelleen käänteisfunktion derivaatta pisteessä 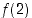 sekä derivoimalla saatu lauseke että ratkaisemalla se funktion
sekä derivoimalla saatu lauseke että ratkaisemalla se funktion 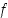 derivaatan avulla.
derivaatan avulla. 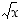 derivaatta.
derivaatta. 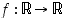 ,
,
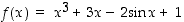 on bijektio. Laske edelleen käänteisfunktion derivaatta jossain valitsemassasi pisteessä.
on bijektio. Laske edelleen käänteisfunktion derivaatta jossain valitsemassasi pisteessä. 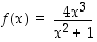
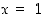 sisältävä väli, jolla funktiolla
sisältävä väli, jolla funktiolla 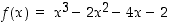 on käänteisfunktio. Määrää käänteisfunktion derivaatta pisteessä
on käänteisfunktio. Määrää käänteisfunktion derivaatta pisteessä 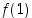 .
. 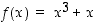 on kaikkialla määritelty käänteisfunktio.
on kaikkialla määritelty käänteisfunktio. 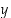 on voimassa epäyhtälö
on voimassa epäyhtälö 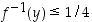 ?
?