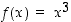 monotonisuus voitiin selvittää ratkaisemalla monotonisuuden ilmaiseva epäyhtälö algebrallisesti. Aina ei kuitenkaan näin voi tehdä. Jos funktio on derivoituva, voidaan derivaattaa käyttää monotonisuuden selvittämiseen.
monotonisuus voitiin selvittää ratkaisemalla monotonisuuden ilmaiseva epäyhtälö algebrallisesti. Aina ei kuitenkaan näin voi tehdä. Jos funktio on derivoituva, voidaan derivaattaa käyttää monotonisuuden selvittämiseen.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Edellisessä esimerkissä funktion 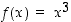 monotonisuus voitiin selvittää ratkaisemalla monotonisuuden ilmaiseva epäyhtälö algebrallisesti. Aina ei kuitenkaan näin voi tehdä. Jos funktio on derivoituva, voidaan derivaattaa käyttää monotonisuuden selvittämiseen.
monotonisuus voitiin selvittää ratkaisemalla monotonisuuden ilmaiseva epäyhtälö algebrallisesti. Aina ei kuitenkaan näin voi tehdä. Jos funktio on derivoituva, voidaan derivaattaa käyttää monotonisuuden selvittämiseen.
Lause 4.3.2. (Derivoituvan funktion monotonisuustesti)
Oletetaan, että funktio 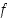 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 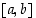 ja derivoituva avoimella välillä
ja derivoituva avoimella välillä 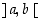 . Tällöin pätevät seuraavat.
. Tällöin pätevät seuraavat.
(a) Jos 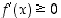 kaikilla
kaikilla 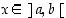 ,
on
,
on 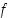 kasvava välillä
kasvava välillä 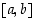 .
.
(b) Jos 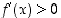 kaikilla
kaikilla 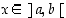 ,
on
,
on 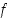 aidosti kasvava välillä
aidosti kasvava välillä 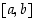 .
.
(c) Jos 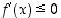 kaikilla
kaikilla 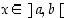 ,
on
,
on 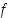 vähenevä välillä
vähenevä välillä 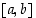 .
.
(d) Jos 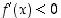 kaikilla
kaikilla 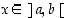 ,
on
,
on 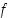 aidosti vähenevä välillä
aidosti vähenevä välillä 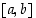 .
.
Todistus. Olkoot 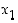 ja
ja 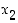 välin
välin 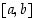 pisteitä, ja olkoon
pisteitä, ja olkoon 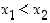 . Silloin differentiaalilaskennan väliarvolauseen perusteella on
. Silloin differentiaalilaskennan väliarvolauseen perusteella on
jollakin 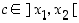 . Soveltamalla kussakin kohdassa oletusta derivaatan arvoon
. Soveltamalla kussakin kohdassa oletusta derivaatan arvoon 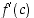 saadaan väitteet.
saadaan väitteet.
Funktiolle 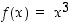 on
on 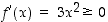 aina, joten
aina, joten 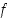 on koko reaalialueella kasvava. Lisäksi
on koko reaalialueella kasvava. Lisäksi 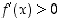 ,
kun
,
kun 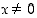 . Tämän perusteella ei voi kuitenkaan vielä päätellä funktion
. Tämän perusteella ei voi kuitenkaan vielä päätellä funktion 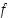 aitoa kasvavuutta koko reaalialueella. Mutta edellä olevaa testiä voidaan käyttää väleillä
aitoa kasvavuutta koko reaalialueella. Mutta edellä olevaa testiä voidaan käyttää väleillä 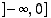 ja
ja 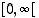 ,
joten näillä väleillä
,
joten näillä väleillä 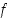 on aidosti kasvava. Yhdistämällä nämä tietoudet saadaan
on aidosti kasvava. Yhdistämällä nämä tietoudet saadaan 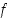 aidosti kasvavaksi koko reaalialueella.
aidosti kasvavaksi koko reaalialueella.
Tarkastellaan funktiota 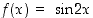 välillä
välillä 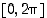 . Funktio
. Funktio 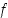 on kaikkialla derivoituva ja
on kaikkialla derivoituva ja 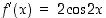 . Tästä näkyy, että tarkasteluvälillä on
. Tästä näkyy, että tarkasteluvälillä on 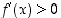 ,
kun
,
kun 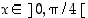 tai kun
tai kun 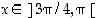 ,
ja toisaalta
,
ja toisaalta 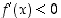 ,
kun
,
kun 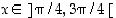 . Siten
. Siten 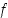 on aidosti kasvava väleillä
on aidosti kasvava väleillä 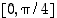 ja
ja 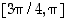 sekä aidosti vähenevä välillä
sekä aidosti vähenevä välillä 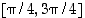 . Koko välillä
. Koko välillä 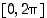 funktio
funktio 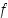 on siten paloittain aidosti monotoninen.
on siten paloittain aidosti monotoninen.
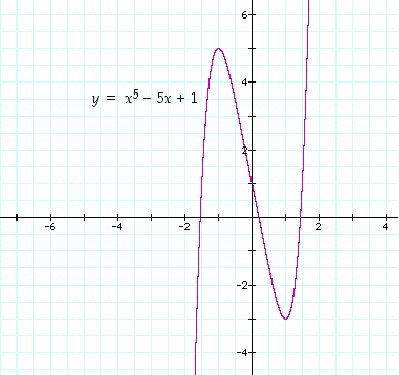
Monotonisuutta voi käyttää funktion nollakohtien lukumäärän selvittämiseen. Tarkastellaan sitä varten funktiota 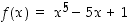 . Tämä polynomi on itse asiassa sellainen, että sen juurille ei ole olemassa mitään juurenotoin ja rationaalisin laskutoimituksin ilmaistavaa lauseketta. Toki juurille voidaan löytää likiarvoja. Tässä selvitämme vain juurien lukumäärän.
. Tämä polynomi on itse asiassa sellainen, että sen juurille ei ole olemassa mitään juurenotoin ja rationaalisin laskutoimituksin ilmaistavaa lauseketta. Toki juurille voidaan löytää likiarvoja. Tässä selvitämme vain juurien lukumäärän.
Funktion 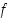 derivaatta on
derivaatta on 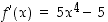 ja tämän nollakohdat ovat
ja tämän nollakohdat ovat 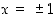 . Jos
. Jos 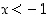 tai
tai 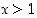 ,
on
,
on 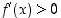 ,
joten
,
joten 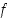 on aidosti kasvava väleillä
on aidosti kasvava väleillä 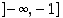 ja
ja 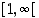 . Jos
. Jos 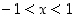 ,
on derivaatta negatiivinen ja siten
,
on derivaatta negatiivinen ja siten 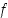 on aidosti vähenevä välillä
on aidosti vähenevä välillä 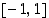 . Funktiolla on siis kolme monotonisuusväliä. Kullakin monotonisuusvälillä funktiolla voi olla vain yksi nollakohta, joten koko funktiolla voi olla korkeintaan kolme nollakohtaa.
. Funktiolla on siis kolme monotonisuusväliä. Kullakin monotonisuusvälillä funktiolla voi olla vain yksi nollakohta, joten koko funktiolla voi olla korkeintaan kolme nollakohtaa.
Selvitetään sitten muuttaako funktio 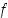 merkkiään kyseisillä monotonisuusväleillä. Koska esimerkiksi
merkkiään kyseisillä monotonisuusväleillä. Koska esimerkiksi
vaihtaa 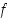 merkkiään jokaisella monotonisuusvälillään ja siten Bolzanon lauseen mukaan funktiolla
merkkiään jokaisella monotonisuusvälillään ja siten Bolzanon lauseen mukaan funktiolla 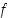 on nollakohta kullakin väleistä
on nollakohta kullakin väleistä 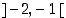 ,
,
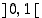 ja
ja 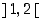 . Funktiolla
. Funktiolla 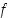 on siis täsmälleen kolme nollakohtaa. Nollakohtien likiarvot ovat −1,54, 0,20 ja 1,44. Katso kuva 40.
on siis täsmälleen kolme nollakohtaa. Nollakohtien likiarvot ovat −1,54, 0,20 ja 1,44. Katso kuva 40.
Opiskeluvideo: D7: Nollakohtien lukumäärä 
