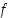 määritelty välillä
määritelty välillä 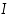 . Funktio
. Funktio 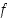 on
on
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tässä pykälässä tarkastellaan funktion kuvaajan nousevuutta ja laskevuutta ja sen selvittämistä derivaatan avulla.
Olkoon funktio 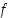 määritelty välillä
määritelty välillä 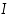 . Funktio
. Funktio 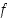 on
on
• kasvava välillä 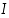 ,
jos ehdosta
,
jos ehdosta 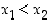 seuraa aina, että
seuraa aina, että 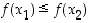 ,
,
• aidosti kasvava välillä 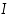 ,
jos ehdosta
,
jos ehdosta 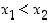 seuraa aina, että
seuraa aina, että 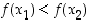 ,
,
• vähenevä välillä 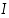 ,
jos ehdosta
,
jos ehdosta 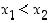 seuraa aina, että
seuraa aina, että 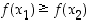 ,
,
• aidosti vähenevä välillä 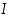 ,
jos ehdosta
,
jos ehdosta 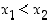 seuraa aina, että
seuraa aina, että 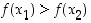 .
.
Yllä olevien ehtojen täytyy siis päteä kaikilla 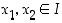 . Kasvavaa funktiota sanotaan myös nousevaksi ja vähenevää vastaavasti laskevaksi. Nämä nimitykset tulevat funktion kuvaajan nousevuudesta ja laskevuudesta.
. Kasvavaa funktiota sanotaan myös nousevaksi ja vähenevää vastaavasti laskevaksi. Nämä nimitykset tulevat funktion kuvaajan nousevuudesta ja laskevuudesta.
Tarkastellaan funktiota 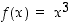 . Olkoon
. Olkoon 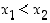 ja lasketaan funktion arvojen erotukseksi
ja lasketaan funktion arvojen erotukseksi
Tässä ensimmäinen tulon termi 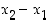 on positiivinen. Toinen tulon termi on neliöiden summana ainakin epänegatiivinen, mutta summaa tarkemmin tarkasteltaessa huomataan, että tämä on nolla vain jos
on positiivinen. Toinen tulon termi on neliöiden summana ainakin epänegatiivinen, mutta summaa tarkemmin tarkasteltaessa huomataan, että tämä on nolla vain jos 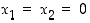 . Siten
. Siten 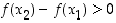 ,
kun
,
kun 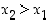 . Funktio
. Funktio 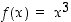 on näin ollen aidosti kasvava koko reaalilukualueella.
on näin ollen aidosti kasvava koko reaalilukualueella.
Funktiota, joka on joko kasvava tai vähenevä, sanotaan monotoniseksi. Vastaavasti aidosti vähenevää ja aidosti kasvavaa funktiota sanotaan aidosti monotoniseksi. Funktio on paloittain (aidosti) monotoninen välillä 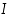 ,
jos väli
,
jos väli 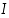 voidaan jakaa äärelliseen määrään osavälejä, joilla kullakin funktio on (aidosti) monotoninen.
voidaan jakaa äärelliseen määrään osavälejä, joilla kullakin funktio on (aidosti) monotoninen.