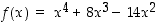Harjoitustehtäviä

136.   Määrää laajimmat mahdolliset välit, joilla funktio 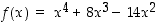on aidosti kasvava.

137.   Alla on kuvattuna erään funktion 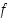kuvaaja välillä 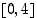. Kuvaaja muodostuu suorasta ja ympyrän kaarista.

(a) Millainen olisi mielestäsi funktion 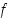lauseke ?

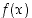(b) Hahmottele derivaatan 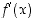kuvaajaa. Päättele se mieluummin kuvaajasta suoraan kuin lausekkeestasi. Kiinnitä huomiota derivaatan nollakohtiin ja merkkiin.

138.   Olkoon

kun 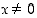, ja olkoon 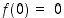. Osoita, et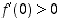tä , mutta 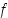ei ole kasvava millään origon sisältävällä välillä.

139.   Oletetaan, että reaalifunktiolla 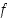on (kaikkialla määritelty) kasvava derivaatta. Osoita, että kiinteällä 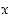funktio

on kasvava välillä .

140.   Tekemällä monotonisuustarkastelu erotusfunktiolle osoita, että epäyhtälö 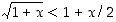pätee aina, kun 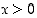. (Vrt. tehtävä 130)

141.   Selvitä, montako reaalijuurta funktiolla 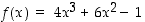on välillä .

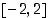142.   Määrää funktiolle 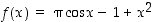kaikki sellaiset välit, joissa se on monotoninen. Hahmottele kuvaajaa.

143.   Osoita differentiaalilaskennan väliarvolauseen avulla, että polynomilla 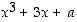on korkeintaan kaksi reaalista juurta (olipa vakio 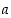mikä tahansa). Osoita edelleen, että tällä polynomilla on itse asiassa täsmälleen yksi reaalinen juuri.

144.   Tutki ensin, millä luvun 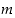arvoilla yhtälöllä 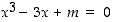on ratkaisu välillä 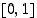. Perustele vastauksesi. Osoita edelleen, että tällä yhtälöllä ei ole koskaan kahta ratkaisua kyseisellä välillä.

145.   Olkoon 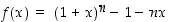, missä 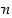on positiivinen kokonaisluku. Osoita, että 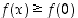aina, kun 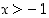. (Vihje: Tutki funktion monotonisuutta.)