Tason 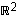 alkio
alkio 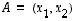 on havainnon mukaan
piste, jonka komponentteja
on havainnon mukaan
piste, jonka komponentteja 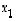 ja
ja 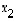 sanotaan myös sen
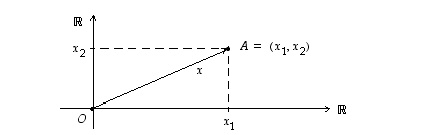
koordinaateiksi. Kun tarkastellaan lineaarisia eli 'suoraviivaisia' ilmiöitä, on usein havainnollisempaa kuvata alkiota
sanotaan myös sen
koordinaateiksi. Kun tarkastellaan lineaarisia eli 'suoraviivaisia' ilmiöitä, on usein havainnollisempaa kuvata alkiota 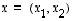 vektorina origosta
vektorina origosta 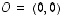 pisteeseen
pisteeseen 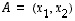 .
.
Tätä tulkintaa käyttäen asetetaan vektorien 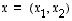 ja
ja 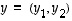 summaksi vektori
summaksi vektori
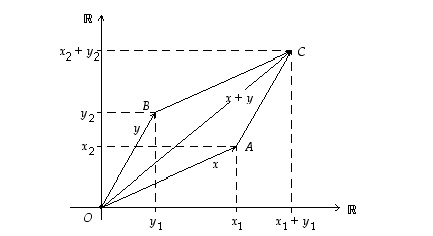
Summan määräytymistä kuvaavassa kuviossa summavektori 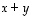 on suunnikkaan
on suunnikkaan 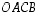 halkaisija,
suuntajana
halkaisija,
suuntajana 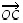 .
.
Jos summassa 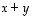 asetetaan
asetetaan 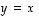 ,
saadaan
,
saadaan
Yleisesti 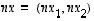 ,
kun
,
kun 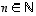 .
Edelleen voidaan sopia, että
.
Edelleen voidaan sopia, että 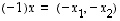 ,
joka on vektorille
,
joka on vektorille 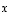 vastakkaissuuntainen, mutta yhtä pitkä vektori. Tästä saadaan samaan tapaan kuin edellä myös kaikilla negatiivisilla kokonaisluvuilla kerrotut vektorit. Tämän jälkeen
vastakkaissuuntainen, mutta yhtä pitkä vektori. Tästä saadaan samaan tapaan kuin edellä myös kaikilla negatiivisilla kokonaisluvuilla kerrotut vektorit. Tämän jälkeen 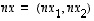 pätee aina, kun
pätee aina, kun 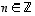 .
.
Kokonaisluvuilla kertomisen suuntaamana asetetaankin jokaiselle reaaliluvulle 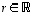 ja jokaiselle vektorille
ja jokaiselle vektorille 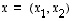 näiden
tuloksi vektori:
näiden
tuloksi vektori:
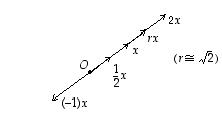
Vaikka
kerroin 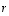 voi olla muukin kuin kokonaisluku eli mikä tahansa reaaliluku, sanotaan vektoria
voi olla muukin kuin kokonaisluku eli mikä tahansa reaaliluku, sanotaan vektoria 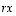 silti yleisesti vektorin
silti yleisesti vektorin 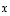 (yleistetyksi)
monikerraksi. (Tarkemmin pitäisi siis puhua reaaliluvun ja vektorin tulosta tai reaaliluvulla kerrotusta vektorista.)
(yleistetyksi)
monikerraksi. (Tarkemmin pitäisi siis puhua reaaliluvun ja vektorin tulosta tai reaaliluvulla kerrotusta vektorista.)
Havainnollistuksissa ajatellaan myös, että vektoria voi esittää mikä tahansa suuntajana, joka on yhtä pitkä ja saman suuntainen kuin origosta lähtevä suuntajana. Suuntajana on siis vektorin edustaja, ilmentymä.
Esimerkiksi alla olevassa, summan muodostumista esittävässä kuvassa vektoria 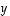 voi esittää sekä suuntajana
voi esittää sekä suuntajana 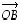 että suuntajana
että suuntajana 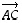 .
Samoin vektoria
.
Samoin vektoria 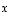 voi esittää sekä suuntajana
voi esittää sekä suuntajana 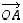 että suuntajana
että suuntajana  .
Vektoreiden yhteenlasku voidaankin havainnollistaa asettamalla vektoreita edustavat suuntajanat 'peräkkäin'.
.
Vektoreiden yhteenlasku voidaankin havainnollistaa asettamalla vektoreita edustavat suuntajanat 'peräkkäin'.
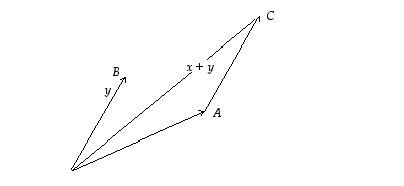
Vektori 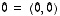 on
nollavektori ja vektori
on
nollavektori ja vektori 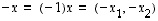 on vektorin
on vektorin 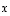 vastavektori. Vektorien
vastavektori. Vektorien 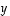 ja
ja 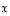 erotus on vektori
erotus on vektori
Vektoreille 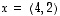 ja
ja 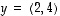 - jotka ovat eri vektorit, koska niiden komponentit ovat eri järjestyksessä - on
- jotka ovat eri vektorit, koska niiden komponentit ovat eri järjestyksessä - on
Piirrä tason vektoreille 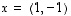 ,
,
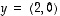 ja
ja 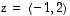 vektorit
vektorit 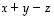 ja
ja 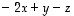 sekä lue kuvasta tulosvektoreiden koordinaatit. Kokeile yhdistellä vektoreita myös eri järjestyksessä. Tarkista tulokset laskemalla kyseiset vektorit.
sekä lue kuvasta tulosvektoreiden koordinaatit. Kokeile yhdistellä vektoreita myös eri järjestyksessä. Tarkista tulokset laskemalla kyseiset vektorit.
Seuraavat tason vektoreita koskevat laskusäännöt on helppo todeta oikeiksi ja se tehtävä jätetäänkin lähes täysin lukijalle.
Tason vektoreille 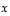 ,
,
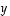 ja
ja 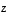 sekä reaaliluvuille
sekä reaaliluvuille 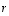 ja
ja 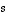 pätevät seuraavat säännöt.
pätevät seuraavat säännöt.
Todistus.
Käydään tässä esimerkkinä läpi vain ensimmäinen kohta. Tason vektoreille 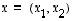 ja
ja 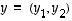 saadaan lukujen yhteenlaskun vaihdannaisuuden perusteella, että
saadaan lukujen yhteenlaskun vaihdannaisuuden perusteella, että
Taso 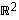 on tällöin esimerkki yleisemmästä struktuurista,
vektoriavaruudesta. Puhutaan myös
lineaariavaruudesta tai
lineaarisesta
avaruudesta. Yleisesti vektoriavaruuksiksi sanotaan mitä tahansa joukkoa, jossa on sillä tavalla määritellyt alkioiden yhteenlasku ja reaaliluvulla kertominen, että lauseessa 2.2 luetellut ominaisuudet täyttyvät.
on tällöin esimerkki yleisemmästä struktuurista,
vektoriavaruudesta. Puhutaan myös
lineaariavaruudesta tai
lineaarisesta
avaruudesta. Yleisesti vektoriavaruuksiksi sanotaan mitä tahansa joukkoa, jossa on sillä tavalla määritellyt alkioiden yhteenlasku ja reaaliluvulla kertominen, että lauseessa 2.2 luetellut ominaisuudet täyttyvät.
Edellisen lauseen mukaan kaikki samantapaiset yhteen- ja kertolaskuja koskevat laskulait kuin luvuille toimivat myös vektoreille ja sen monikerroille. Yleisen käytännön mukaisesti monikerrassa vain luku kirjoitetaan aina vektorin vasemmalle puolelle: kirjoitetaan siis 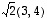 eikä
eikä 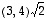 .
.
Jos 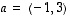 ja
ja 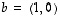 ,
voidaan yhtälöstä
,
voidaan yhtälöstä 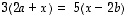 vektori
vektori 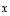 ratkaista edellä olevia laskulakeja käyttäen esimerkiksi seuraavasti:
ratkaista edellä olevia laskulakeja käyttäen esimerkiksi seuraavasti:
Huomioi, että tässä yhtälö ratkaistiin pitämällä vektorit ensin yleisinä ja vasta lopussa sijoitettiin niiden konkreettiset arvot.
Osoitetaan, että suunnikkaan halkaisijat puolittavat toisensa. Olkoon suunnikkaassa 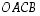 vektori
vektori 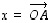 ja vektori
ja vektori 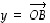 .
.
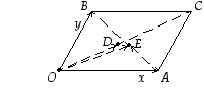 Suuntajanan
Suuntajanan 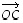 keskipiste
keskipiste 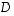 on silloin suuntajanan
on silloin suuntajanan 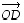 eli vektorin
eli vektorin
päätepiste. Suuntajana 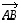 taas edustaa vektoria
taas edustaa vektoria 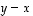 ja sen keskipiste
ja sen keskipiste 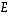 on suuntajanan
on suuntajanan 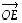 eli vektorin
eli vektorin
päätepiste. Keskipisteet ovat siten saman suuntajanan päätepisteinä samat. Tämä yhteinen piste on näin ollen halkaisijoiden leikkauspiste ja puolittaa ne molemmat.
Määrää luvut 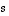 ja
ja 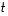 niin, että
niin, että 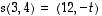 .
Tee se sekä laskemalla että geometrisesti.
.
Tee se sekä laskemalla että geometrisesti.
Tasossa 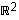 akselien suuntaisilla vektoreilla
akselien suuntaisilla vektoreilla
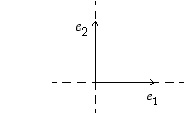
on erityisiä ominaisuuksia: Ensinnäkin, jos 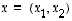 on mielivaltainen tason vektori, niin
on mielivaltainen tason vektori, niin
Jokainen vektori 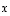 voidaan siis esittää vektoreiden
voidaan siis esittää vektoreiden 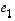 ja
ja 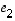 ns.
lineaarikombinaationa
ns.
lineaarikombinaationa
Toiseksi tämä esitys on yksikäsitteinen: jos kerrointa 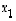 tai
tai 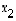 muutetaan, summa (eli vektori
muutetaan, summa (eli vektori 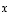 ) muuttuu myös.
) muuttuu myös.
Sanotaan, että vektorit 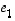 ja
ja 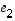 muodostavat tason
muodostavat tason 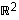 luonnollisen
kannan.
Niiden lineaarikombinaationa voidaan siis esittää jokainen tason vektori ja lisäksi kukin vain yhdellä tavalla (eli vain yksin kertoimin).
luonnollisen
kannan.
Niiden lineaarikombinaationa voidaan siis esittää jokainen tason vektori ja lisäksi kukin vain yhdellä tavalla (eli vain yksin kertoimin).
Usein käytetään luonnollisen kannan vektoreista myös merkintöjä 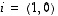 ja
ja 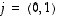 ,
jolloin siis jokaisella vektorilla
,
jolloin siis jokaisella vektorilla 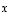 on myös esitys
on myös esitys