Avaruus

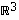
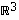
Av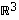aruuden kolmikoille 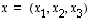ja 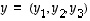sekä luvulle 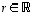asetetaan, samaan tapaan kuin tasossa, summaksi ja monikerraksi kolmikot

ja
.

Avaruus 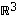on nyt myös vektoriavaruus, sillä lauseessa 2.2 mainitut säännöt pätevät senkin vektoreille. Nollavektori on nyt 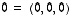ja vektorin 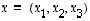vastavektori on vektori 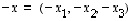. Kuten tasossa vektoria 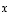havainnollistetaan suuntajanana origosta 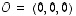pisteeseen .

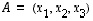Avaruudessa 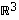luonnollisen kannan muodostavat vektorit

sillä jokainen vektori 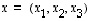voidaan yksikäsitteisesti esittää lineaarikombinaationa

.

Kertoimi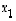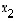a , ja 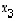sanotaan myös vektorin 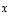koordinaateiksi. Kantavektorit kuvataan usein oikean käden systeemin mukaan, jolloin ne suuntautuvat avaruudessa kuten oikean käden peukalo, etusormi ja keskisormi.