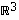
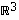
Avaruudessa 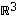 (ja vain siinä!) voidaan tuottaa yksi lisäoperaatio vektoreille, jonka avulla saadaan ratkaistua eräitä ortogonaalisuuteen ja muitakin geometriaan liittyviä kysymyksiä.
(ja vain siinä!) voidaan tuottaa yksi lisäoperaatio vektoreille, jonka avulla saadaan ratkaistua eräitä ortogonaalisuuteen ja muitakin geometriaan liittyviä kysymyksiä.
Muodostetaan vektoreille 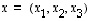 ja
ja 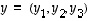 vektori
vektori 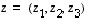 ,
missä
,
missä
Vektori 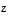 on vektoreiden
on vektoreiden 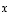 ja
ja 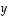 vektoritulo (tai
ristitulo), merkitään
vektoritulo (tai
ristitulo), merkitään 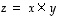 .
Muodollisesti se saadaan seuraavalla tavalla determinantista
.
Muodollisesti se saadaan seuraavalla tavalla determinantista
kun käytetään determinantin kehityssääntöä (ikäänkuin vektorit 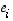 olisivat lukuja) ensimmäisen rivin suhteen ja merkitään muodostettavat alideterminantit luonnollisten kantavektorien kertoimiksi.
olisivat lukuja) ensimmäisen rivin suhteen ja merkitään muodostettavat alideterminantit luonnollisten kantavektorien kertoimiksi.
Seuraavassa on nippu vektoritulon ominaisuuksia. Ne kaikki ovat periaatteessa helppoja todistaa laskemalla, mutta todistukset sivuutetaan tässä.
Avaruuden 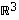 vektoreille
vektoreille 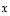 ,
,
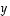 ja
ja 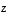 pätevät seuraavat:
pätevät seuraavat:
(1) 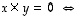
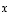 ja
ja 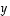 ovat lineaarisesti riippuvat,
ovat lineaarisesti riippuvat,
(7)  ,
kun
,
kun 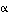 on vektorien
on vektorien 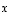 ja
ja 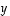 välinen kulma,
välinen kulma,
Vektorit 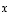 ,
,
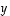 ja
ja 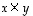 muodostavat aina ns.
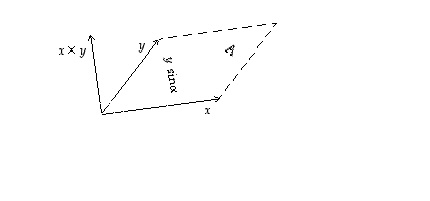
oikean käden systeemin eli ne suuntautuvat avaruudessa kuten oikean käden peukalo, etusormi ja keskisormi. Lisäksi kohdan (7) mukaan vektorin
muodostavat aina ns.
oikean käden systeemin eli ne suuntautuvat avaruudessa kuten oikean käden peukalo, etusormi ja keskisormi. Lisäksi kohdan (7) mukaan vektorin 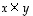 pituus on vektorien
pituus on vektorien 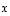 ja
ja 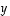 virittämän suunnikkaan ala.
virittämän suunnikkaan ala.
Esimerkissä 10.7 laskettiin vektoreiden 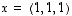 ja
ja 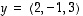 vektorituloksi
vektorituloksi 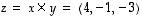 .
Sisätulon avulla nähdään heti, että saatu vektori
.
Sisätulon avulla nähdään heti, että saatu vektori 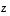 on todella kohtisuorassa kumpaakin vektoria vastaan. Sen lisäksi tiedetään nyt, että vektorien
on todella kohtisuorassa kumpaakin vektoria vastaan. Sen lisäksi tiedetään nyt, että vektorien 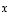 ja
ja 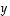 virittämän suunnikkaan ala on sama kuin vektorin
virittämän suunnikkaan ala on sama kuin vektorin 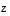 pituus
pituus 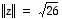 .
.