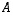 on mielivaltainen
on mielivaltainen 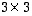 -matriisi ja
-matriisi ja 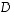 diagonaalimatriisi, jonka lävistäjäalkiot ovat 2, 3 ja 4. Muodosta tulot
diagonaalimatriisi, jonka lävistäjäalkiot ovat 2, 3 ja 4. Muodosta tulot 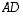 ja
ja 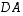 .
Mitä diagonaalimatriisilla kertomista koskevia sääntöjä voit päätellä tuloksista?
.
Mitä diagonaalimatriisilla kertomista koskevia sääntöjä voit päätellä tuloksista?
1. Olkoon 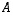 on mielivaltainen
on mielivaltainen 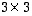 -matriisi ja
-matriisi ja 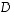 diagonaalimatriisi, jonka lävistäjäalkiot ovat 2, 3 ja 4. Muodosta tulot
diagonaalimatriisi, jonka lävistäjäalkiot ovat 2, 3 ja 4. Muodosta tulot 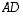 ja
ja 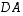 .
Mitä diagonaalimatriisilla kertomista koskevia sääntöjä voit päätellä tuloksista?
.
Mitä diagonaalimatriisilla kertomista koskevia sääntöjä voit päätellä tuloksista?
2. Tarkastellaan seuraavista kolmesta matriisista
saatavia matriisilausekkeita. Jos 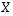 ,
,
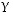 ja
ja 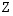 voidaan valita samoiksikin matriiseiksi, selvitä mitkä muotoa
voidaan valita samoiksikin matriiseiksi, selvitä mitkä muotoa 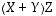 olevat lausekkeet on määritelty ja laske sitten ne (yhteensä selvitettävänä on 27 eri mahdollisuutta).
olevat lausekkeet on määritelty ja laske sitten ne (yhteensä selvitettävänä on 27 eri mahdollisuutta).
3. Tehtävänäsi on seuraavassa kuvatulla menettelyllä johtaa sinin ja kosinin summakulmakaavat (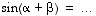 ja
ja 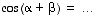 ). Olkoon
). Olkoon 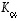 tason kierto kulman
tason kierto kulman 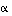 verran (jolloin
verran (jolloin 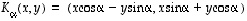 ).
).
(a) Muodosta lineaarikuvausta 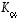 vastaava matriisi
vastaava matriisi 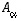 .
.
(b) Muodosta tason kiertoa kulman 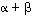 verran vastaava matriisi
verran vastaava matriisi 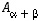 .
.
(c) Muodosta yhdistettyä lineaarikuvausta 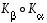 vastaava matriisi.
vastaava matriisi.
(d) Vertaa kohtien (b) ja (c) tuloksia keskenään.
4. Millä luvun 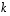 arvoilla matriisitulot
arvoilla matriisitulot 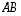 ja
ja 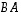 ovat samat, kun
ovat samat, kun
5. Keksi jokin sellainen matriisista 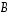 eroava matriisi
eroava matriisi 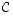 ,
että
,
että 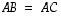 (vaikka
(vaikka 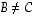 ), kun
), kun
käänteismatriisi. (Tarkista tulos!)
7. Etsi käänteismatriisit matriiseille
8. Määrää lineaarikuvauksen 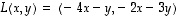 käänteiskuvaus.
käänteiskuvaus.
9. Määrää Gaussin ja Jordanin menetelmällä käänteismatriisi matriisille
10. Määrää alla olevan matriisin 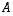 käänteismatriisi ja ratkaise sen avulla matriisi
käänteismatriisi ja ratkaise sen avulla matriisi 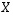 alla olevasta yhtälöstä:
alla olevasta yhtälöstä:
11. Määrää sellainen kerroin 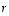 ,
että matriisi
,
että matriisi 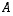 on ortogonaalinen, kun
on ortogonaalinen, kun
12. Määrää seuraavan matriisin 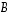 käänteismatriisi:
käänteismatriisi:
Vihje: Voit tehdä sen esimerkiksi Gaussin ja Jordanin menetelmällä. Mutta voit ratkaista tehtävän myös toisin, kun ensin mietit missä mielessä matriisi 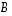 on erikoinen! Vrt. edellinen tehtävä.
on erikoinen! Vrt. edellinen tehtävä.