Matriisien tulo
Selvitetään seuraavaksi, millaiset matriisit vastaavat yhdistettyjä kuvauksia. Johdannoksi palataan ensin aikaisempaan esimerkkiin.
Esimerkki 8.1.
Tarkastellaan esimerkin 7.2 lineaarikuvauksia 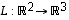 ,
,
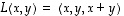 ,
ja
,
ja 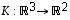 ,
,
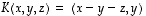 .
Luonnollisissa kannoissa niitä vastaavat matriisit
.
Luonnollisissa kannoissa niitä vastaavat matriisit
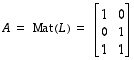
ja
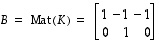 .
.
Yhdistetty kuvaus 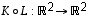 on silloin lineaarikuvaus, jolle
on silloin lineaarikuvaus, jolle
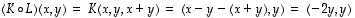 .
.
Tason luonnollisessa kannassa sitä vastaa siten matriisi
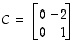 .
.
Tämän esimerkin tapauksessa myös yhdistetty kuvaus 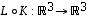 on määritelty. Sen lauseke on
on määritelty. Sen lauseke on
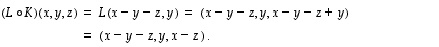
joten avaruuden  luonnollisessa kannassa sitä vastaa matriisi
luonnollisessa kannassa sitä vastaa matriisi
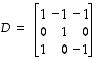 .
.
Herää varmasti kysymys, voitaisiinko matriisit 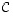 ja
ja 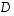 jotenkin määrätä matriiseista
jotenkin määrätä matriiseista 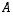 ja
ja 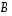 .
Mutta miten sen voisi tehdä?
.
Mutta miten sen voisi tehdä?

Olkoot nyt yleisesti 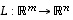 ja
ja 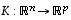 (mahdollisesti eri avaruuksien välisiä) lineaarikuvauksia sekä
(mahdollisesti eri avaruuksien välisiä) lineaarikuvauksia sekä 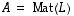 ja
ja 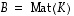 niitä vastaavat
niitä vastaavat 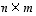 - ja
- ja 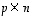 -matriisit. Yhdistetty kuvaus
-matriisit. Yhdistetty kuvaus 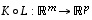 on silloin määritelty. Aikaisemmin todetun lauseen 6.9 mukaan se on edelleen lineaarikuvaus. Selvitetään nyt, millainen matriisi sitä vastaava matriisi
on silloin määritelty. Aikaisemmin todetun lauseen 6.9 mukaan se on edelleen lineaarikuvaus. Selvitetään nyt, millainen matriisi sitä vastaava matriisi 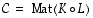 on.
on.
Tätä varten on selvitettävä kantavektorien kuvien koordinaatit. Määrätään ensin ensimmäisen kantavektorin kuva 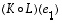 .
Koska
.
Koska
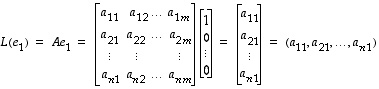 ,
,
on
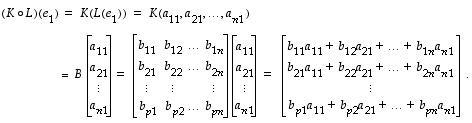
Lineaarikuvausta  vastaavan matriisin
vastaavan matriisin 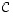 ensimmäinen sarake saadaan siten kertomalla matriisilla
ensimmäinen sarake saadaan siten kertomalla matriisilla 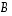 matriisin
matriisin 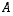 ensimmäisen sarakkeen vektori.
ensimmäisen sarakkeen vektori.
Voidaan todeta, että vastaavasti menetellen saadaan muutkin matriisin 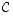 sarakkeet. Ne muodostetaan siis kertomalla matriisilla
sarakkeet. Ne muodostetaan siis kertomalla matriisilla 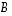 vuoron perään matriisin
vuoron perään matriisin 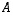 sarakkeet. Sanotaankin, että koko matriisi
sarakkeet. Sanotaankin, että koko matriisi 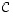 on matriisien
on matriisien 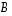 ja
ja 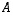 tulo ja merkitään, että
tulo ja merkitään, että
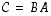 .
.
Yllä on todistettu seuraava tulos.
Esimerkki 8.4.
Edellä esimerkeissä 7.2 ja 8.1 todettiin, että lineaarikuvauksia 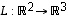 ,
,
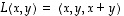 ,
ja
,
ja 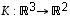 ,
,
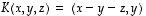 vastaavat luonnollisissa kannoissa matriisit
vastaavat luonnollisissa kannoissa matriisit
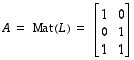
ja
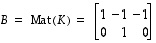 .
.
Yhdistettyä kuvausta 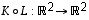 vastaa siten matriisi
vastaa siten matriisi
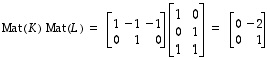 .
.
Saatiin sama matriisi kuin esimerkissä 8.1. Lisäksi tuloksesta nähdään, että 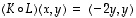 .
.
Myös yhdistettyä kuvausta 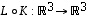 vastaa sama matriisi kuin mainitussa esimerkissäkin laskettiin:
vastaa sama matriisi kuin mainitussa esimerkissäkin laskettiin:
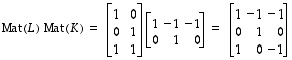 .
.

Esimerkki 8.5.
Venytys ja vinoutus -esimerkissä 6.4 venytys oli kuvaus 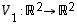 ,
jolle
,
jolle
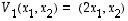 ,
,
ja vinoutus taas kuvaus 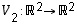 ,
jolle
,
jolle
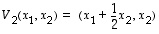 .
.
Näistä yhdistämällä saatu venytys ja vinoutus oli edelleen yhdistetty kuvaus 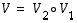 ,
jolle
,
jolle 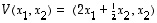 .
Näitä kolmea lineaarikuvausta vastaavat matriisit
.
Näitä kolmea lineaarikuvausta vastaavat matriisit
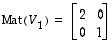 ,
,
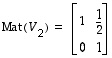
ja
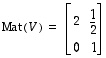 .
.
Toisaalta pätee - kuten pitääkin -
 .
.

Seuraavassa on matriiseille eräitä laskusääntöjä, jotka on periaatteessa helppo todeta muodostamalla esiintyvien matriisien alkiot. Sivuutetaan näiden varsin suoraviivaiset, mutta osin pitkähköt, todistukset tässä. Merkki 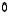 edustaa nollamatriisia, jonka kaikki luvut ovat nollia, ja
edustaa nollamatriisia, jonka kaikki luvut ovat nollia, ja 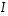 yksikkömatriisia, joka vastaa identtistä kuvausta ja jossa siten on ykköset paikoissa
yksikkömatriisia, joka vastaa identtistä kuvausta ja jossa siten on ykköset paikoissa 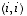 ja nollat muualla.
ja nollat muualla.
Lause 8.6.
Kun matriisien 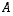 ,
,
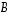 ja
ja 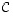 tyypit ovat kussakin tapauksessa sellaiset, että alla esiintyvät laskutoimitukset ovat määriteltyjä, seuraavat säännöt pätevät.
tyypit ovat kussakin tapauksessa sellaiset, että alla esiintyvät laskutoimitukset ovat määriteltyjä, seuraavat säännöt pätevät.
(1) 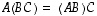 ,
,
(2) 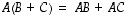 ,
,
(3) 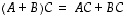 ,
,
(4) 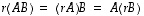 kaikilla
kaikilla 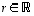 ,
,
(5) 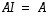 ja
ja 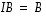 ,
,
(6) 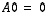 ja
ja 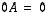 .
.
Aikaisemmin esimerkin 8.3 jälkeen huomautettiin siitä, että matriisitulo ei ole vaihdannainen operaatio. Huomaa myös, että matriisitulo voi olla nollamatriisi ilman, että kumpikaan tekijöistä on nollamatriisi. Tällaisen tilanteen antavat esimerkiksi matriisit
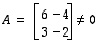
ja
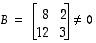 ,
,
joille
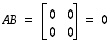 .
.
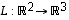 ,
,
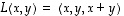 ,
ja
,
ja 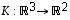 ,
,
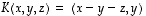 .
Luonnollisissa kannoissa niitä vastaavat matriisit
.
Luonnollisissa kannoissa niitä vastaavat matriisit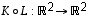 on silloin lineaarikuvaus, jolle
on silloin lineaarikuvaus, jolle 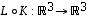 on määritelty. Sen lauseke on
on määritelty. Sen lauseke on 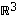 luonnollisessa kannassa sitä vastaa matriisi
luonnollisessa kannassa sitä vastaa matriisi 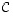 ja
ja 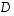 jotenkin määrätä matriiseista
jotenkin määrätä matriiseista 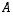 ja
ja 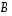 .
Mutta miten sen voisi tehdä?
.
Mutta miten sen voisi tehdä? 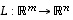 ja
ja 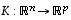 (mahdollisesti eri avaruuksien välisiä) lineaarikuvauksia sekä
(mahdollisesti eri avaruuksien välisiä) lineaarikuvauksia sekä 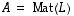 ja
ja 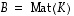 niitä vastaavat
niitä vastaavat 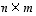 - ja
- ja 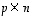 -matriisit. Yhdistetty kuvaus
-matriisit. Yhdistetty kuvaus 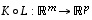 on silloin määritelty. Aikaisemmin todetun lauseen 6.9 mukaan se on edelleen lineaarikuvaus. Selvitetään nyt, millainen matriisi sitä vastaava matriisi
on silloin määritelty. Aikaisemmin todetun lauseen 6.9 mukaan se on edelleen lineaarikuvaus. Selvitetään nyt, millainen matriisi sitä vastaava matriisi 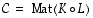 on.
on. 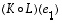 .
Koska
.
Koska  vastaavan matriisin
vastaavan matriisin 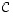 ensimmäinen sarake saadaan siten kertomalla matriisilla
ensimmäinen sarake saadaan siten kertomalla matriisilla 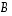 matriisin
matriisin 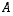 ensimmäisen sarakkeen vektori.
ensimmäisen sarakkeen vektori. 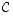 sarakkeet. Ne muodostetaan siis kertomalla matriisilla
sarakkeet. Ne muodostetaan siis kertomalla matriisilla 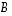 vuoron perään matriisin
vuoron perään matriisin 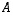 sarakkeet. Sanotaankin, että koko matriisi
sarakkeet. Sanotaankin, että koko matriisi 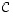 on matriisien
on matriisien 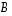 ja
ja 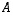 tulo ja merkitään, että
tulo ja merkitään, että 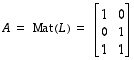
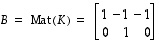 .
.
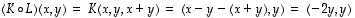 .
.
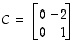 .
.
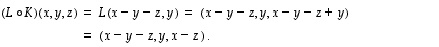
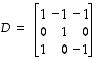 .
.

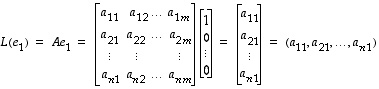 ,
,
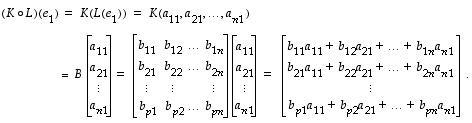
 .
.
 ja
ja  on
on 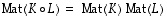 .
.
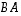 on määritelty vain, kun matriisin
on määritelty vain, kun matriisin 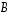 sarakkeita on täsmälleen yhtä monta kuin matriisissa
sarakkeita on täsmälleen yhtä monta kuin matriisissa 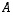 on rivejä:
on rivejä: 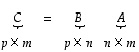
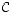 on yhtä monta riviä kuin matriisissa
on yhtä monta riviä kuin matriisissa 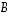 ja yhtä monta saraketta kuin matriisissa
ja yhtä monta saraketta kuin matriisissa 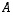 .
.
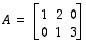
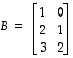
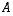 on tyyppiä
on tyyppiä 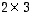 ja matriisi
ja matriisi 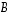 tyyppiä
tyyppiä 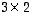 ,
joten tulomatriisi
,
joten tulomatriisi 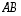 on olemassa ja on tyyppiä
on olemassa ja on tyyppiä 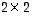 .
Tulomatriisi on
.
Tulomatriisi on  .
.
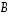 on tyyppiä
on tyyppiä 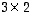 ja
ja 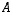 tyyppiä
tyyppiä 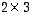 ,
joten myös tulo
,
joten myös tulo 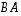 on olemassa, on tyyppiä
on olemassa, on tyyppiä 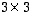 ja on
ja on  .
.

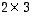 ja toinen tyyppiä
ja toinen tyyppiä 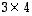 .
Nämä matriisit voidaan kertoa mainitussa järjestyksessä (
.
Nämä matriisit voidaan kertoa mainitussa järjestyksessä ( 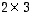 kertaa
kertaa 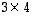 ), mutta ei päinvastaisessa järjestyksessä (
), mutta ei päinvastaisessa järjestyksessä ( 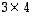 kertaa
kertaa 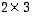 ).
). 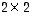 -matriisia
-matriisia 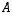 ja
ja 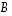 ,
että
,
että 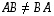 .
.
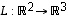 ,
,
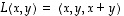 ,
ja
,
ja 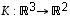 ,
,
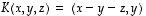 vastaavat luonnollisissa kannoissa matriisit
vastaavat luonnollisissa kannoissa matriisit 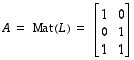
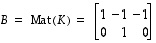 .
.
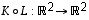 vastaa siten matriisi
vastaa siten matriisi 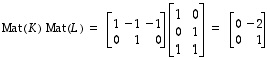 .
.
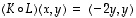 .
.
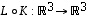 vastaa sama matriisi kuin mainitussa esimerkissäkin laskettiin:
vastaa sama matriisi kuin mainitussa esimerkissäkin laskettiin: 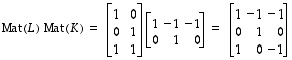 .
.

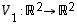 ,
jolle
,
jolle 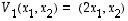 ,
,
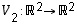 ,
jolle
,
jolle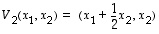 .
.
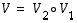 ,
jolle
,
jolle 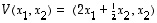 .
Näitä kolmea lineaarikuvausta vastaavat matriisit
.
Näitä kolmea lineaarikuvausta vastaavat matriisit 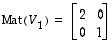 ,
,
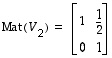
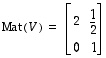 .
.
 .
.

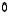 edustaa nollamatriisia, jonka kaikki luvut ovat nollia, ja
edustaa nollamatriisia, jonka kaikki luvut ovat nollia, ja 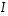 yksikkömatriisia
yksikkömatriisia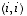 ja nollat muualla.
ja nollat muualla. 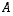 ,
,
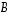 ja
ja 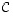 tyypit ovat kussakin tapauksessa sellaiset, että alla esiintyvät laskutoimitukset ovat määriteltyjä, seuraavat säännöt pätevät.
tyypit ovat kussakin tapauksessa sellaiset, että alla esiintyvät laskutoimitukset ovat määriteltyjä, seuraavat säännöt pätevät. 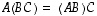 ,
,
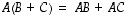 ,
,
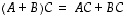 ,
,
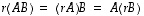 kaikilla
kaikilla 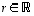 ,
,
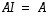 ja
ja 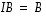 ,
,
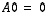 ja
ja 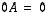 .
.
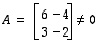
 ,
,
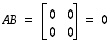 .
.
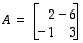
 ,
että
,
että 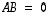 .
.