Matriisien summa ja monikerta
Selvitetään seuraavaksi, miten summakuvauksia ja monikertakuvauksia vastaavat matriisit saadaan alkuperäisiä vastaavista matriiseista.
Olkoot taas 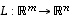 ja
ja 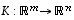 (samojen avaruuksien välisiä) lineaarikuvauksia sekä
(samojen avaruuksien välisiä) lineaarikuvauksia sekä 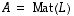 ja
ja 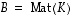 niitä vastaavat matriisit. Lineaarikuvausten
niitä vastaavat matriisit. Lineaarikuvausten 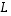 ja
ja 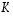 summa
summa 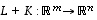 ja kuvauksen
ja kuvauksen 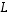 monikerta
monikerta 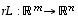 määritellään, kuten edellisessä luvussa jo tehtiinkin, asettamalla kaikilla vektoreilla
määritellään, kuten edellisessä luvussa jo tehtiinkin, asettamalla kaikilla vektoreilla 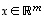
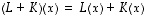 ja
ja 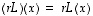 (
( 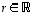 ).
).
Molemmat on lauseessa 6.11 todettu lineaarikuvauksiksi. On helppo nähdä, että summakuvausta 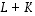 vastaa silloin
summamatriisi
vastaa silloin
summamatriisi
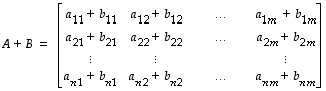
ja monikertaa 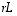 ,
missä
,
missä 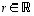 ,
monikertamatriisi
,
monikertamatriisi
 .
.
Sama tulos voidaan ilmaista myös toisin:
Esimerkki 7.6.
Esimerkiksi
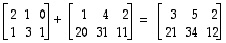 ja
ja
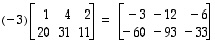 .
.

Seuraavassa on joukko varsin ilmeisiä sääntöjä lineaarikuvauksien ja matriisien lineaarisille yhdistämisille. Todistukset sivuutetaan helppoina ja ilmeisinä. Lauseen kohdissa A 3-4 merkki 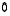 edustaa
nollakuvausta ja
nollamatriisia vastaavasti. Edellinen kuvaa kaikki vektorit nollavektoriksi ja jälkimmäisessä kaikki sen alkiot ovat nollia.
edustaa
nollakuvausta ja
nollamatriisia vastaavasti. Edellinen kuvaa kaikki vektorit nollavektoriksi ja jälkimmäisessä kaikki sen alkiot ovat nollia.
Esimerkki 7.8.
Matriisiyhtälöstä 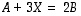 voidaan ylläolevien sääntöjen avulla ratkaista matriisi
voidaan ylläolevien sääntöjen avulla ratkaista matriisi 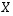 (kun kaikki esiintyvät matriisit ovat keskenään samantyyppisiä):
(kun kaikki esiintyvät matriisit ovat keskenään samantyyppisiä):

Konkreeteille matriiseille
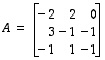 ja
ja 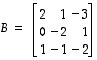
ratkaisuna on siten
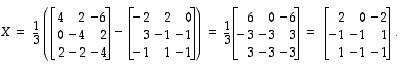

Havainnollistus: Matriisitulo
Opiskelutehtävä 28
Matriiseille
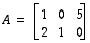 ja
ja 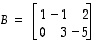
(a) laske matriisi 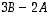 ja
ja
(b) ratkaise matriisi 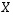 yhtälöstä
yhtälöstä 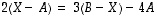 .
.
Vinkki tehtävään 28
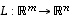 ja
ja 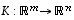 (samojen avaruuksien välisiä) lineaarikuvauksia sekä
(samojen avaruuksien välisiä) lineaarikuvauksia sekä 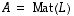 ja
ja 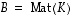 niitä vastaavat matriisit. Lineaarikuvausten
niitä vastaavat matriisit. Lineaarikuvausten 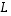 ja
ja 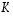 summa
summa 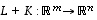 ja kuvauksen
ja kuvauksen 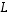 monikerta
monikerta 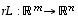 määritellään, kuten edellisessä luvussa jo tehtiinkin, asettamalla kaikilla vektoreilla
määritellään, kuten edellisessä luvussa jo tehtiinkin, asettamalla kaikilla vektoreilla 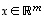
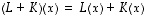 ja
ja 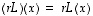 (
(  ).
). 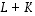 vastaa silloin
summamatriisi
vastaa silloin
summamatriisi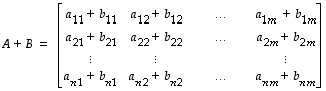
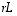 ,
missä
,
missä 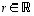 ,
monikertamatriisi
,
monikertamatriisi .
.
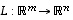 ja
ja 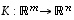 sekä luvulle
sekä luvulle 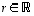 on
on 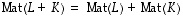 ja
ja 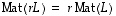 .
.
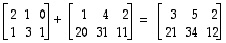 ja
ja 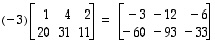 .
.

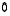 edustaa
nollakuvausta
edustaa
nollakuvausta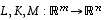 ja niitä vastaaville
ja niitä vastaaville 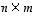 -matriiseille
-matriiseille 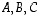 sekä reaaliluvuille
sekä reaaliluvuille 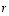 ja
ja 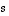 pätevät seuraavat säännöt.
pätevät seuraavat säännöt. 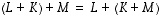
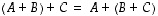
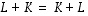
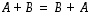
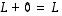
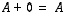
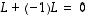
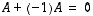
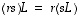
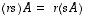
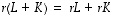
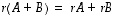
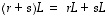
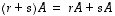
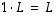
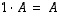
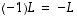
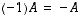
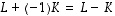
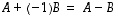
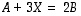 voidaan ylläolevien sääntöjen avulla ratkaista matriisi
voidaan ylläolevien sääntöjen avulla ratkaista matriisi 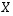 (kun kaikki esiintyvät matriisit ovat keskenään samantyyppisiä):
(kun kaikki esiintyvät matriisit ovat keskenään samantyyppisiä): 
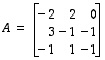 ja
ja 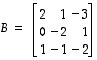
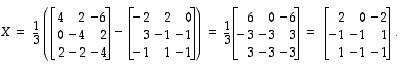

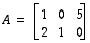 ja
ja 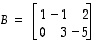
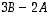 ja
ja 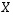 yhtälöstä
yhtälöstä 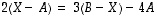 .
.