Kuvaus
Aluksi kerrataan luettelonomaisesti muutamia perusasioita kuvauksista.
·
Funktio eli
kuvaus 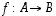 on sääntö (relaatio), joka liittää kuhunkin
lähtöjoukon eli
määrittelyjoukon
on sääntö (relaatio), joka liittää kuhunkin
lähtöjoukon eli
määrittelyjoukon 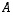 alkioon
alkioon 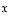 yhden (ja vain yhden)
maalijoukon
yhden (ja vain yhden)
maalijoukon 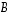 alkion
alkion 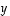 .
Tätä yhteyttä merkitään
.
Tätä yhteyttä merkitään 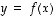 ja alkiota
ja alkiota 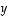 sanotaan alkion
sanotaan alkion 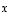 kuvaksi tai funktion
kuvaksi tai funktion 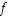 arvoksi pisteessä
arvoksi pisteessä 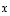 .
.
· Kuvauksessa 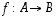 osajoukon
osajoukon 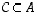 kuva(joukko) on kaikkien joukon
kuva(joukko) on kaikkien joukon 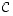 alkioiden kuvien muodostama joukko
alkioiden kuvien muodostama joukko
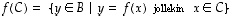 .
.
· Edellisestä erikoistapauksena funktion 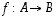 kuvajoukko eli
arvojoukko on koko joukon
kuvajoukko eli
arvojoukko on koko joukon 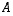 kuvajoukko
kuvajoukko
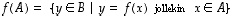 .
.
· Osajoukon 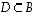 alkukuva on joukon
alkukuva on joukon 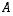 osajoukko
osajoukko
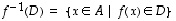 .
.
· Edellisestä erikoistapauksena alkion 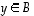 alkukuva on
alkukuva on
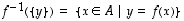 .
.
· Funktio 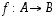 on
injektio, jos se kuvaa kaikki alkiot eri alkioiksi ts. jos
on
injektio, jos se kuvaa kaikki alkiot eri alkioiksi ts. jos 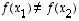 aina, kun
aina, kun 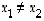 .
On sama asia vaatia, että ehdosta
.
On sama asia vaatia, että ehdosta 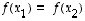 seuraa aina, että
seuraa aina, että 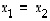 .
.
· Funktio 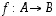 on
surjektio (eli
epijektio), jos sen kuvajoukko on koko maalijoukko ts. jos jokaiselle
on
surjektio (eli
epijektio), jos sen kuvajoukko on koko maalijoukko ts. jos jokaiselle 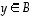 löytyy
löytyy 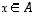 niin, että
niin, että 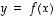 .
.
· Funktio 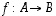 on
bijektio, jos se on sekä injektio että surjektio eli jos jokaista
on
bijektio, jos se on sekä injektio että surjektio eli jos jokaista 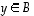 vastaa täsmälleen yksi
vastaa täsmälleen yksi 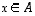 ,
jolle
,
jolle 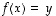 .
.
·
Identtinen
kuvaus on kuvaus 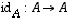 ,
jolle
,
jolle 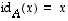 kaikilla
kaikilla 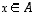 .
.
· Funktioiden 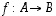 ja
ja 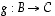 yhdistetty
kuvaus on se kuvaus
yhdistetty
kuvaus on se kuvaus 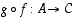 ,
jolle
,
jolle 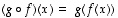 kaikille
kaikille 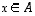 .
.
· Bijektion 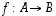 käänteiskuvaus on se kuvaus
käänteiskuvaus on se kuvaus 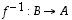 ,
jolle
,
jolle 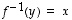 silloin, kun
silloin, kun 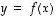 .
On yhtäpitävää vaatia, että
.
On yhtäpitävää vaatia, että 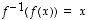 kaikilla
kaikilla 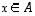 ja
ja 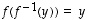 kaikilla
kaikilla 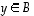 .
Nämä ehdot voidaan ilmoittaa myös muodossa
.
Nämä ehdot voidaan ilmoittaa myös muodossa 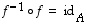 ja
ja 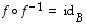 .
.
· Kahden bijektion 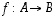 ja
ja 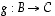 yhdistetty kuvaus
yhdistetty kuvaus 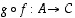 on myös bijektio. Tällöin
on myös bijektio. Tällöin 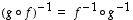 .
.
Esimerkki 6.1.
Kuvaus 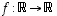 ,
,
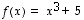 ,
on bijektio. Käy läpi sen injektiivisyys ja surjektiivisuus! Sen käänteiskuvaus on
,
on bijektio. Käy läpi sen injektiivisyys ja surjektiivisuus! Sen käänteiskuvaus on 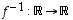 ,
jolle
,
jolle 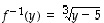 .
.
Jos lisäksi 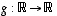 on kuvaus, jolle
on kuvaus, jolle 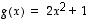 (joka muuten ei ole bijektio), saadaan yhdistetyksi kuvaukseksi kuvaus
(joka muuten ei ole bijektio), saadaan yhdistetyksi kuvaukseksi kuvaus
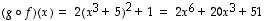 .
.
Tässä esimerkkitapauksessa myös yhdistetty kuvaus 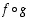 on määritelty ja sen lauseke on
on määritelty ja sen lauseke on
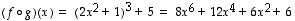 .
.
Kumpikaan yhdistetyistä funktioista ei ole bijektio.

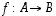 on sääntö (relaatio), joka liittää kuhunkin
lähtöjoukon eli
määrittelyjoukon
on sääntö (relaatio), joka liittää kuhunkin
lähtöjoukon eli
määrittelyjoukon 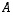 alkioon
alkioon 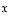 yhden (ja vain yhden)
maalijoukon
yhden (ja vain yhden)
maalijoukon 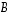 alkion
alkion 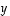 .
Tätä yhteyttä merkitään
.
Tätä yhteyttä merkitään 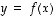 ja alkiota
ja alkiota 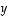 sanotaan alkion
sanotaan alkion 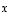 kuvaksi tai funktion
kuvaksi tai funktion 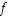 arvoksi pisteessä
arvoksi pisteessä 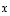 .
.
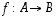 osajoukon
osajoukon 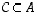 kuva(joukko)
kuva(joukko)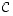 alkioiden kuvien muodostama joukko
alkioiden kuvien muodostama joukko 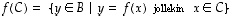 .
.
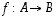 kuvajoukko
kuvajoukko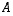 kuvajoukko
kuvajoukko 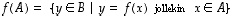 .
.
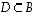 alkukuva
alkukuva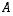 osajoukko
osajoukko 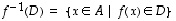 .
.
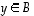 alkukuva
alkukuva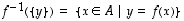 .
.
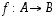 on
injektio
on
injektio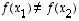 aina, kun
aina, kun 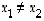 .
On sama asia vaatia, että ehdosta
.
On sama asia vaatia, että ehdosta 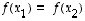 seuraa aina, että
seuraa aina, että 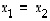 .
.
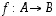 on
surjektio
on
surjektio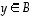 löytyy
löytyy 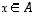 niin, että
niin, että 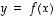 .
.
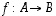 on
bijektio
on
bijektio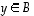 vastaa täsmälleen yksi
vastaa täsmälleen yksi 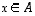 ,
jolle
,
jolle 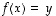 .
.
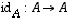 ,
jolle
,
jolle 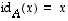 kaikilla
kaikilla 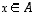 .
.
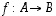 ja
ja 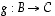 yhdistetty
yhdistetty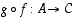 ,
jolle
,
jolle 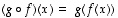 kaikille
kaikille 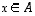 .
.
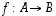 käänteiskuvaus
käänteiskuvaus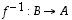 ,
jolle
,
jolle 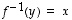 silloin, kun
silloin, kun 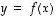 .
On yhtäpitävää vaatia, että
.
On yhtäpitävää vaatia, että 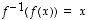 kaikilla
kaikilla 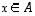 ja
ja 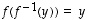 kaikilla
kaikilla 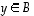 .
Nämä ehdot voidaan ilmoittaa myös muodossa
.
Nämä ehdot voidaan ilmoittaa myös muodossa 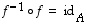 ja
ja 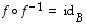 .
.
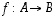 ja
ja 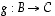 yhdistetty kuvaus
yhdistetty kuvaus 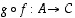 on myös bijektio. Tällöin
on myös bijektio. Tällöin 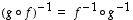 .
.
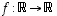 ,
,
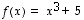 ,
on bijektio. Käy läpi sen injektiivisyys ja surjektiivisuus! Sen käänteiskuvaus on
,
on bijektio. Käy läpi sen injektiivisyys ja surjektiivisuus! Sen käänteiskuvaus on 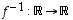 ,
jolle
,
jolle 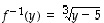 .
.
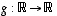 on kuvaus, jolle
on kuvaus, jolle 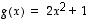 (joka muuten ei ole bijektio), saadaan yhdistetyksi kuvaukseksi kuvaus
(joka muuten ei ole bijektio), saadaan yhdistetyksi kuvaukseksi kuvaus 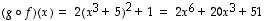 .
.
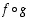 on määritelty ja sen lauseke on
on määritelty ja sen lauseke on 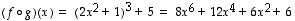 .
.
