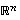 kahdelle vektorille voidaan määrätä ensimmäisen projektio toiselle eli löytää toisen suuntainen vektori, jonka kärkipiste on mahdollisimman lähellä ensimmäisen kärkipistettä.
kahdelle vektorille voidaan määrätä ensimmäisen projektio toiselle eli löytää toisen suuntainen vektori, jonka kärkipiste on mahdollisimman lähellä ensimmäisen kärkipistettä.
Selvitetään seuraavassa, miten avaruuden 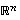 kahdelle vektorille voidaan määrätä ensimmäisen projektio toiselle eli löytää toisen suuntainen vektori, jonka kärkipiste on mahdollisimman lähellä ensimmäisen kärkipistettä.
kahdelle vektorille voidaan määrätä ensimmäisen projektio toiselle eli löytää toisen suuntainen vektori, jonka kärkipiste on mahdollisimman lähellä ensimmäisen kärkipistettä.
Olkoot 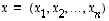 ja
ja 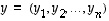 tarkasteltavat vektorit. Etsitään vektorin
tarkasteltavat vektorit. Etsitään vektorin 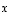 suuntaista vektoria
suuntaista vektoria 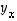 ,
jonka kärkipiste on mahdollisimman lähellä vektorin
,
jonka kärkipiste on mahdollisimman lähellä vektorin 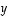 kärkipistettä. Merkitään ensin, että
kärkipistettä. Merkitään ensin, että
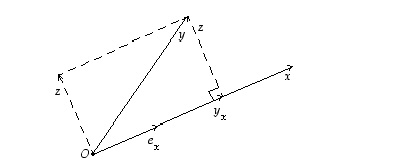
Vektori 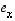 on siten vektorin
on siten vektorin 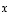 suuntainen yksikkövektori. Vektorin
suuntainen yksikkövektori. Vektorin 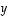 projektiota vektorille
projektiota vektorille 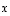 on siis etsittävä muodossa
on siis etsittävä muodossa 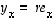 .
Sellainen löydetäänkin asettamalla
.
Sellainen löydetäänkin asettamalla
Osoitetaan tämän toimivuus. Merkitsemällä 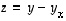 saadaan, että
saadaan, että
joten 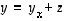 ,
missä
,
missä 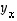 on vektorin
on vektorin 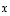 suuntainen ja
suuntainen ja 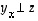 .
.
sanotaan vektorin 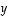 projektioksi vektorille
projektioksi vektorille 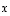 (tai tarkemmin sen suuntaiselle suoralle).
(tai tarkemmin sen suuntaiselle suoralle).
Vektorin 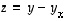 pituus ilmoittaa vektorin
pituus ilmoittaa vektorin 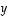 (kärkipisteen) etäisyyden vektorin
(kärkipisteen) etäisyyden vektorin 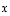 määräämästä suorasta
määräämästä suorasta 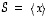 .
.
Projektion avulla nähdään edelleen, miten vektoreiden välinen kulma määräytyy, sillä nyt
(merkki määräytyy sen mukaan, onko kulma terävä vai tylppä). Saatiin siis se kaava, jolla kulma aikaisemmin määriteltiinkin.
Määrätään tasossa ensin vektorin 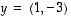 projektio vektorille
projektio vektorille 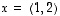 .
Koska
.
Koska 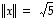 ,
niin
,
niin 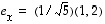 .
Edelleen
.
Edelleen 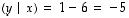 ,
joten kysytty projektio on
,
joten kysytty projektio on
Tätä projektiota vastaan kohtisuora vektori on
Tämän vektorin pituus 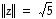 on vektorin
on vektorin 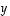 (kärkipisteen) etäisyys vektorin
(kärkipisteen) etäisyys vektorin 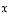 määräämästä suorasta. Vektoreiden
määräämästä suorasta. Vektoreiden 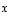 ja
ja 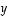 väliselle kulmalle
väliselle kulmalle 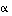 on edelleen voimassa, että
on edelleen voimassa, että
joten 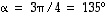 .
Piirrä kuva tilanteesta ruutupaperille!
.
Piirrä kuva tilanteesta ruutupaperille!
Vektorin projektio voidaan yleisemmin määritellä vektorin sijasta kyllä aliavaruuksillekin. Selvitetään se lähemmin vain 2-ulotteisille aliavaruuksille eli tasoille.
Olkoot 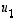 ja
ja 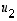 kaksi lineaarisesti riippumatonta avaruuden
kaksi lineaarisesti riippumatonta avaruuden 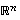 vektoria, jolloin ne virittävät avaruudessa kaksiulotteisen aliavaruuden eli tason
vektoria, jolloin ne virittävät avaruudessa kaksiulotteisen aliavaruuden eli tason 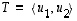 .
Projektion laskemista varten määrätään ensin kyseiseen tasoon ortonormaali kanta seuraavasti.
.
Projektion laskemista varten määrätään ensin kyseiseen tasoon ortonormaali kanta seuraavasti.
Valitaan ensimmäiseksi vektoriksi
jolloin se on vektorin 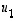 suuntainen yksikkövektori.
suuntainen yksikkövektori.
Määrätään sitten vektorin 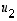 projektion avulla vektori
projektion avulla vektori
Silloin 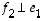 ja toisaalta vektorit
ja toisaalta vektorit 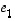 ja
ja 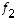 määräävät saman tason kuin
määräävät saman tason kuin 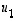 ja
ja 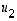 ,
sillä näiden lineaarikombinaatiot antavat selvästi samat vektorit. Valitsemalla lopuksi
,
sillä näiden lineaarikombinaatiot antavat selvästi samat vektorit. Valitsemalla lopuksi
saadaan kyseiselle tasolle 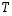 ortonormaali kanta
ortonormaali kanta 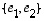 .
.
Vektorin 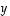 projektio
tasolle
projektio
tasolle 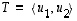 saadaan nyt lausekkeesta
saadaan nyt lausekkeesta
Silloin erotusvektori 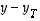 on todella koko tasoa
on todella koko tasoa 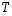 vastaan kohtisuorassa, sillä
vastaan kohtisuorassa, sillä
Koko tasoa vastaan kohtisuoruutta varten riittää nimittäin kohtisuoruuden lineaarisuuden takia todeta kohtisuoruus tason virittäjävektoreita vastaan.
Vektorin 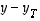 pituus ilmoittaa vektorin
pituus ilmoittaa vektorin 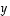 (kärkipisteen) etäisyyden tasosta
(kärkipisteen) etäisyyden tasosta 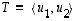 .
.
Huomaa, että projektion kaavan käytössä on olennaista, että  on kyseisen tason ortonormaali kanta.
on kyseisen tason ortonormaali kanta.
(a) kahden koordinaattiakselin määräämälle tasolle (Huom! Tästä tulee 3 eri tapausta) ja
(b) tasolle 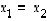 eli sille tasolle jonka virittävät esimerkiksi vektorit
eli sille tasolle jonka virittävät esimerkiksi vektorit 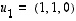 ja
ja 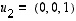 .
.