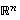vektoreiden 
,
,
..., 
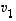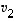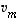sanotaan olevan keskenään
ortogonaaliset eli
kohtisuorassa toisiaan vastaan, jos 
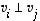aina kun 
.
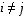Toisaalta vektoria 
,
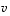jonka pituus 
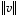on yksi, sanotaan
yksikkövektoriksi.
Avaruuden 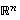vektoreiden ,
,
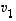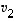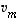..., sanotaan olevan keskenään
ortogonaaliset eli
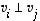kohtisuorassa toisiaan vastaan, jos aina kun .
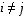Toisaalta vektoria ,
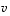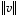jonka pituus on yksi, sanotaan
yksikkövektoriksi.
Avaruuden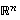 
kanta 
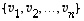on siten
ortogonaalinen, jos kaikki sen vektorit ovat kohtisuorassa toisiaan vastaan. Se on
ortonormaali, jos ortogonaalisuuden lisäksi vektoreiden pituudet ovat ykkösiä. Kanta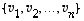 
on näin ollen ortonormaali, jos 
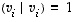kaikilla indekseillä ja 
,
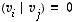kun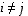 
.
Avaruuksien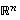 
luonnolliset kannat ovat ortonormaaleja kantoja. Ne ovat nimittäin kaikki ykkösen pituisia ja kohtisuorassa toisiaan vastaan.
Tasossa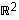 
vektorit 
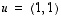ja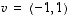 
ovat keskenään ortogonaaliset, sillä 
.
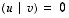Ne ovat myös lineaarisesti riippumattomat, joten ne muodostavat ortogonaalisen kannan. Ne eivät kuitenkaan muodosta ortonormaalia kantaa, sillä niiden pituudet eivät ole ykkösiä. Niistä saadaan kuitenkin muodostettua helposti ortonormaali kanta '
normittamalla' ne ts. jakamalla ne pituuksillaan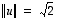 
ja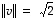 
.
Saadut vektorit
Määrää tasoon sellainen ortogonaalinen kanta, jonka ensimmäinen vektori on vektorin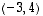 
suuntainen. Tee se sekä laskemalla että graafisesti. Miten saat siitä ortonormaalin kannan?
Keskenään ortogonaaliset, nollasta eroavat vektorit ovat aina lineaarisesti riippumattomat.
Todistus.
Olkoot avaruuden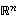 
vektorit 
,
,
..., 
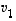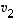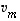keskenään ortogonaaliset. Merkitään niiden lineaarikombinaatio nollaksi,
ja osoitetaan, että siinä kaikki kertoimet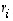 
ovat nollia. Lasketaan ensin vektorin 
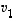ja yllä olevan lineaarikombinaation sisätulo. Koska 
,
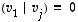kun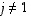 
,
saadaan tulokseksi vain yhtälö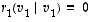 
.
Tässä 
,
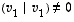koska vektori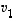 
oletettiin nollasta eroavaksi. Siten 
.
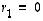Samalla tavalla päätellään muidenkin indeksien osalta. Siten tarkastellun lineaarikombinaation kaikki kertoimet ovat nollia, mikä osoittaa, että vektorit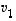 
,
,
..., 
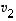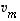ovat lineaarisesti riippumattomat.
Koska yllä olevan lauseen mukaan keskenään ortogonaaliset vektorit ovat välttämättä lineaarisesti riippumattomat, niitä ei voi olla koskaan avaruuden dimensiota enempää. Toisaalta, jos niitä on täsmälleen dimension verran, ne muodostavat silloin ortogonaalisen kannan.
,
