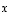 ,
jotka ovat kohtisuorassa vektoria
,
jotka ovat kohtisuorassa vektoria 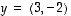 vastaan.
vastaan.
1. Ilmoita kaikki ne tason vektorit 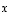 ,
jotka ovat kohtisuorassa vektoria
,
jotka ovat kohtisuorassa vektoria 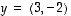 vastaan.
vastaan.
2. Laske vektorien 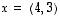 ja
ja 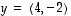 pituudet sekä niiden etäisyys ja välinen kulma.
pituudet sekä niiden etäisyys ja välinen kulma.
3. Osoita, että vektorit 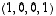 ,
,
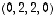 ,
,
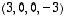 ja
ja 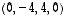 muodostavat avaruuden
muodostavat avaruuden 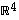 kannan. Mieti erilaisia todistustapoja väitteelle. Miten saisit sen perusteltua mahdollisimman helposti?
kannan. Mieti erilaisia todistustapoja väitteelle. Miten saisit sen perusteltua mahdollisimman helposti?
4. Täydennä vektorit 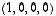 ,
,
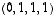 avaruuden
avaruuden 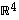 kannaksi. Mieti erilaisia täydennysvaihtoehtoja. Miten saisit sen tehtyä mahdollisimman helposti?
kannaksi. Mieti erilaisia täydennysvaihtoehtoja. Miten saisit sen tehtyä mahdollisimman helposti?
5. Selvitä, mitkä seuraavista vektoripareista ovat kohtisuorassa toisiaan vastaan:
Määrää edelleen kaikille vektoripareille niiden (kärkipisteiden) etäisyydet.
6. Millä luvun 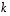 arvoilla vektorit
arvoilla vektorit 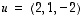 ja
ja 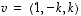
(b) ovat kohtisuorassa toisiaan vastaan,
(c) muodostavat keskenään 45 asteen kulman?
7. Muodosta avaruuteen 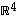 jokin sellainen ortogonaalinen kanta, jonka ensimmäinen kantavektori on vektorin
jokin sellainen ortogonaalinen kanta, jonka ensimmäinen kantavektori on vektorin 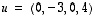 suuntainen. Muokkaa siitä edelleen ortonormaali kanta.
suuntainen. Muokkaa siitä edelleen ortonormaali kanta.
8. Määrää avaruuden 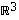 pisteen
pisteen 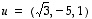 etäisyys ehdon
etäisyys ehdon 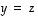 (
( 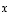 mielivaltainen) määräämästä tasosta (eli tasosta, jonka pisteillä toiset ja kolmannet koordinaatit yhtyvät).
mielivaltainen) määräämästä tasosta (eli tasosta, jonka pisteillä toiset ja kolmannet koordinaatit yhtyvät).
9. Avaruuden 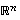 aliavaruudelle
aliavaruudelle 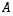 ns.
ortogonaalinen
aliavaruus on joukko
ns.
ortogonaalinen
aliavaruus on joukko
Todista, että tämä joukko on todella aliavaruus. (Tee tämä osoittamalla, että se sisältää vektoriensa lineaarikombinaatiot. Tähän taas riittää, että se sisältää vektoriensa summat ja monikerrat.)