Lause 5.3.
Avaruuden 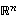 vektoreille
vektoreille 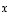 ,
,
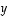 ja
ja 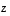 sekä reaaliluvulle
sekä reaaliluvulle 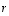 pätevät seuraavat säännöt.
pätevät seuraavat säännöt.
(N4) Jos 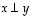 ,
niin
,
niin 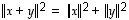 Pythagoras´n lause
Pythagoras´n lause
(SN2) 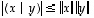 CBS-epäyhtälö (CBS = Cauchy, Bunjakowski & Schwarz)
CBS-epäyhtälö (CBS = Cauchy, Bunjakowski & Schwarz)
Todistus. Käydään läpi tässä vain kohdat (S2), (SN2), (N3) ja (N4) - tässä järjestyksessä. Muut kohdat ovat helppoja tai selväpiirteisiä todentaa.
(S2) Todistetaan ensimmäinen yhtälö suoraviivaisesti laskien:
Toinen yhtälö todistetaan vastaavasti.
(SN2) Olkoon 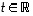 ja tarkastellaan apuvektoria
ja tarkastellaan apuvektoria 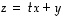 .
Silloin
.
Silloin
Tässä viimeisen epäyhtälön vasen puoli on muuttujan 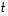 suhteen toisen asteen polynomi. Tällaisella, muotoa
suhteen toisen asteen polynomi. Tällaisella, muotoa 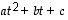 olevalla lausekkeella on nollakohta vain, jos sen diskriminantti
olevalla lausekkeella on nollakohta vain, jos sen diskriminantti 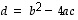 on positiivinen tai nolla. Koska yllä saadussa lausekkeessa neliön
on positiivinen tai nolla. Koska yllä saadussa lausekkeessa neliön 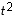 kerroin
kerroin 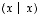 on ei-negatiivinen, on koko lauseke näin ollen ei-negatiivinen täsmälleen silloin, kun sen diskriminantti ei ole positiivinen. Siten edellä oleva on edelleen yhtäpitävää seuraavan kanssa:
on ei-negatiivinen, on koko lauseke näin ollen ei-negatiivinen täsmälleen silloin, kun sen diskriminantti ei ole positiivinen. Siten edellä oleva on edelleen yhtäpitävää seuraavan kanssa:
Näin saadusta yhtäpitävyydestä näkyy, että epäyhtälö 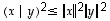 pitää aina paikkansa, kuten väitettiin.
pitää aina paikkansa, kuten väitettiin.
(N3) Todistetaan väite suoraviivaisesti laskien ja jo todistettua kohtaa (SN2) hyväksi käyttäen:
(N4) Edellisen kohdan todistuksesta näkyy, että oletuksen 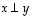 eli ehdon
eli ehdon 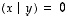 jälkeen
jälkeen
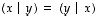
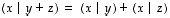
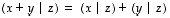
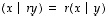
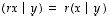
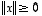 ja
ja 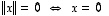
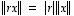
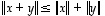 Kolmioepäyhtälö
Kolmioepäyhtälö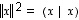
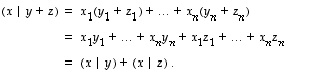
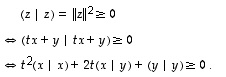
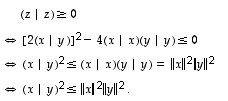
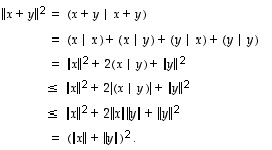
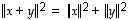 ,
,

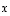 ja
ja 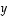 kolmion vierekkäiset sivut sekä olkoon
kolmion vierekkäiset sivut sekä olkoon 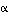 näiden välinen kulma. Tällöin
näiden välinen kulma. Tällöin 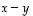 muodostaa kolmannen sivun.
muodostaa kolmannen sivun. 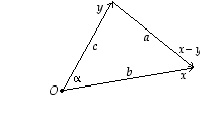 Sen pituuden neliölle saadaan
Sen pituuden neliölle saadaan 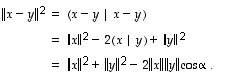
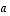 ,
,
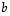 ja
ja 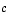 saadaan tämä ehkä yleisemmin tunnettuun kosinilauseen muotoon:
saadaan tämä ehkä yleisemmin tunnettuun kosinilauseen muotoon: 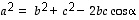 .
.

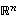 vektoreille
vektoreille 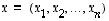 ja
ja 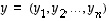 niiden kärkipisteiden etäisyyttä eli lukua
niiden kärkipisteiden etäisyyttä eli lukua 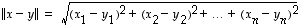
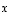 ja
ja 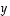 etäisyydeksi
etäisyydeksi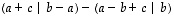 ,
kun tiedetään, että
,
kun tiedetään, että 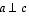 .
.