Sisätulo, vektorien kohtisuoruus ja pituus
Johdannoksi tarkastellaan ensin, milloin tason kaksi vektoria 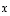 ja
ja 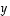 ovat kohtisuorassa, merkitään
ovat kohtisuorassa, merkitään 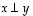 ,
ja samalla yleisemmin, miten näiden välinen kulma voidaan laskea. Olkoot
,
ja samalla yleisemmin, miten näiden välinen kulma voidaan laskea. Olkoot 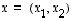 ja
ja 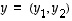 sekä
sekä 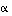 näiden välinen kulma. Koska geometrisesti on selvää, että vektoria
näiden välinen kulma. Koska geometrisesti on selvää, että vektoria 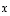 vastaan kohtisuorassa on vektori
vastaan kohtisuorassa on vektori 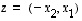 (ks. oheinen kuva), saadaan vektoreiden
(ks. oheinen kuva), saadaan vektoreiden 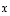 ja
ja 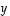 kohtisuoruudelle komponenttien avulla lausuttuna seuraava ehto
kohtisuoruudelle komponenttien avulla lausuttuna seuraava ehto
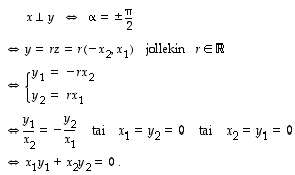
Kun oletetaan luonnollisesti, että 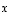 ei ole nollavektori, muodostavat vektorit
ei ole nollavektori, muodostavat vektorit 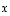 ja
ja 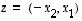 tason kannan ja niiden esitykset luonnollisessa kannassa ovat
tason kannan ja niiden esitykset luonnollisessa kannassa ovat
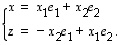
Näistä voidaan ratkaista vektoreille 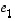 ja
ja 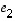 esitykset vektoreiden
esitykset vektoreiden 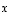 ja
ja 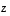 avulla: Kerrotaan ensin edellinen yhtälö luvulla
avulla: Kerrotaan ensin edellinen yhtälö luvulla 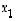 ja jälkimmäinen luvulla
ja jälkimmäinen luvulla 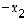 sekä kerrotaan sitten edellinen yhtälö luvulla
sekä kerrotaan sitten edellinen yhtälö luvulla 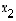 ja jälkimmäinen luvulla
ja jälkimmäinen luvulla 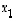 .
Yhteenlaskujen jälkeen saadaan, että
.
Yhteenlaskujen jälkeen saadaan, että
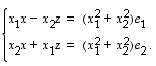
Näistä ratkaistuina saadaan
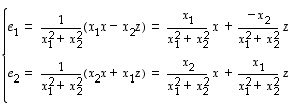
ja edelleen
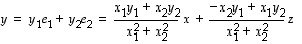 .
.
Näin ollen vektorin  koordinaateiksi
koordinaateiksi  ja
ja 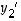 kannassa
kannassa  on saatu luvut
on saatu luvut
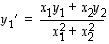
ja
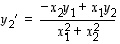 .
.
Vektorien 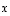 ja
ja 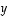 välisen kulman
välisen kulman 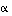 suuruus saadaan edelleen määrättyä ehdosta
suuruus saadaan edelleen määrättyä ehdosta
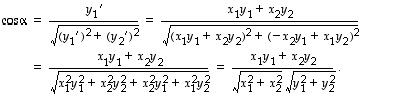
Tuloksena on siten kaiken kaikkiaan, että lausekkeiden
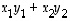 ,
,
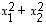 ja
ja 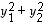
avulla saadaan selvitettyä kohtisuoruuksien lisäksi kulmatkin. Huomaa, että toinen ja kolmas lauseke saadaan ensimmäisestä sijoittamalla vektorit 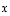 ja
ja 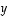 samoiksi.
samoiksi.
Yllä tarkastellun tasotapauksen viitoittamana asetetaankin yleisemmin seuraavasti.
Avaruuden 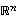 vektorien
vektorien 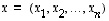 ja
ja 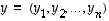 sisätulo (nimeltään myös
pistetulo tai
skalaaritulo) on reaaliluku
sisätulo (nimeltään myös
pistetulo tai
skalaaritulo) on reaaliluku
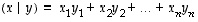 .
.
Muita yleisesti käytettyjä merkintöjä ovat mm. 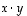 ,
,
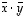 ,
,
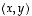 ,
,
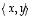 ja
ja 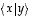 .
.
Edelleen määritellään, että vektorit 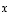 ja
ja 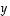 ovat
kohtisuorassa toisiaan vastaan, merkitään
ovat
kohtisuorassa toisiaan vastaan, merkitään 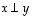 ,
jos
,
jos 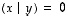 .
.
Esimerkki 5.1.
Vektorien 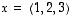 ja
ja 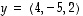 sisätulo on
sisätulo on
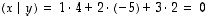 ,
,
joten ne ovat kohtisuorassa toisiaan vastaan. Yritä hahmottaa, jos mahdollista, niiden sijaintia avaruudessa ja vakuuttua geometrisesti niiden kohtisuoruudesta!

Esimerkki 5.2.
Vektoreille 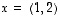 ja
ja 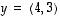 on
on
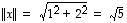 ,
,
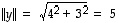 ,
,
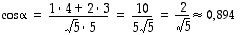 ja
ja
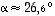 .
.

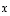 ja
ja 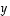 ovat kohtisuorassa, merkitään
ovat kohtisuorassa, merkitään 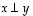 ,
ja samalla yleisemmin, miten näiden välinen kulma voidaan laskea. Olkoot
,
ja samalla yleisemmin, miten näiden välinen kulma voidaan laskea. Olkoot 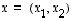 ja
ja 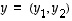 sekä
sekä 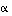 näiden välinen kulma. Koska geometrisesti on selvää, että vektoria
näiden välinen kulma. Koska geometrisesti on selvää, että vektoria 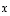 vastaan kohtisuorassa on vektori
vastaan kohtisuorassa on vektori 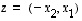 (ks. oheinen kuva), saadaan vektoreiden
(ks. oheinen kuva), saadaan vektoreiden 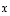 ja
ja 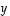 kohtisuoruudelle komponenttien avulla lausuttuna seuraava ehto
kohtisuoruudelle komponenttien avulla lausuttuna seuraava ehto 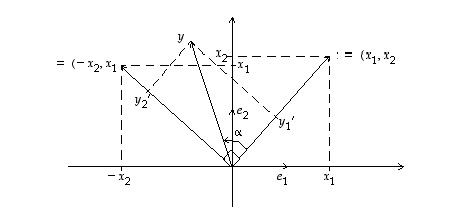
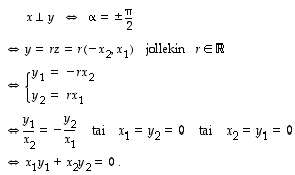
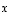 ei ole nollavektori, muodostavat vektorit
ei ole nollavektori, muodostavat vektorit 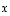 ja
ja 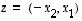 tason kannan ja niiden esitykset luonnollisessa kannassa ovat
tason kannan ja niiden esitykset luonnollisessa kannassa ovat 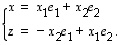
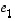 ja
ja 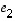 esitykset vektoreiden
esitykset vektoreiden 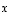 ja
ja 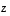 avulla: Kerrotaan ensin edellinen yhtälö luvulla
avulla: Kerrotaan ensin edellinen yhtälö luvulla 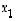 ja jälkimmäinen luvulla
ja jälkimmäinen luvulla 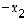 sekä kerrotaan sitten edellinen yhtälö luvulla
sekä kerrotaan sitten edellinen yhtälö luvulla 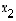 ja jälkimmäinen luvulla
ja jälkimmäinen luvulla 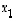 .
Yhteenlaskujen jälkeen saadaan, että
.
Yhteenlaskujen jälkeen saadaan, että 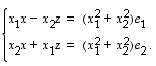
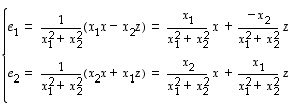
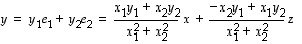 .
.
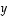 koordinaateiksi
koordinaateiksi 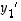 ja
ja 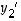 kannassa
kannassa 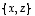 on saatu luvut
on saatu luvut 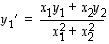
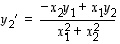 .
.
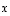 ja
ja 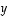 välisen kulman
välisen kulman 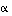 suuruus saadaan edelleen määrättyä ehdosta
suuruus saadaan edelleen määrättyä ehdosta 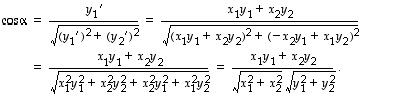
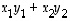 ,
,
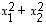 ja
ja 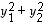
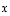 ja
ja 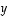 samoiksi.
samoiksi. 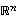 vektorien
vektorien 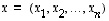 ja
ja 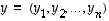 sisätulo
sisätulo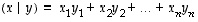 .
.
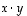 ,
,
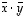 ,
,
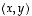 ,
,
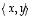 ja
ja 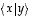 .
.
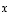 ja
ja 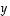 ovat
kohtisuorassa
ovat
kohtisuorassa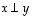 ,
jos
,
jos 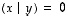 .
.
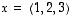 ja
ja 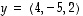 sisätulo on
sisätulo on 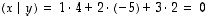 ,
,

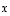 ,
jotka ovat kohtisuorassa vektoreita
,
jotka ovat kohtisuorassa vektoreita 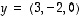 ja
ja 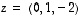 vastaan.
vastaan. 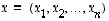 pituus
pituus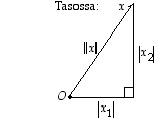 on ei-negatiivinen luku
on ei-negatiivinen luku 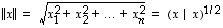
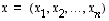 ja
ja 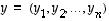 välinen
kulma
välinen
kulma 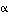 määräytyy ehdosta
määräytyy ehdosta 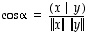 (
( 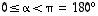 ).
). 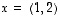 ja
ja 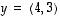 on
on 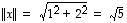 ,
,
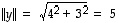 ,
,
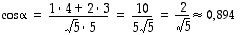 ja
ja 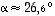 .
.
