Lause 4.18.
Jos vektorijoukko 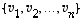 on avaruuden
on avaruuden 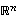 kanta, kukin vektori
kanta, kukin vektori 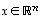 voidaan esittää yksikäsitteisesti niiden lineaarikombinaationa eli muodossa
voidaan esittää yksikäsitteisesti niiden lineaarikombinaationa eli muodossa
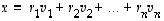 .
.
Todistus.
Koska oletuksen mukaan 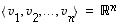 ,
kyseisiä esityksiä on aina olemassa. Olkoon sitten vektorilla
,
kyseisiä esityksiä on aina olemassa. Olkoon sitten vektorilla 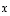 myös toinen esitys
myös toinen esitys
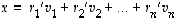 .
.
Silloin saadaan, että
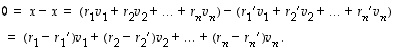
Koska vektorit 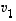 ,
,
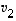 ,
...,
,
..., 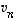 ovat lineaarisesti riippumattomat, yllä saadussa yhtälössä niiden kertoimet ovat kaikki nollia. Siten
ovat lineaarisesti riippumattomat, yllä saadussa yhtälössä niiden kertoimet ovat kaikki nollia. Siten 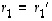 ,
,
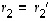 ,
...,
,
..., 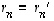 .
Vektorin
.
Vektorin 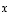 esitykset ovat näin ollen samat.
esitykset ovat näin ollen samat.

Edellä mainittu esitys
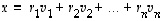
on vektorin 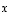 koordinaattiesitys kannassa
koordinaattiesitys kannassa 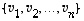 ja luvut
ja luvut 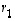 ,
,
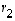 ,
...,
,
..., 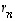 ovat sen
koordinaatit tässä kannassa.
ovat sen
koordinaatit tässä kannassa.
Esimerkki 4.19.
Oletetaan, että 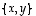 on jokin - mikä tahansa - tason kanta.
on jokin - mikä tahansa - tason kanta.
(a) Osoitetaan ensin, että myös vektorit 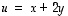 ja
ja 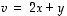 muodostavat aina kannan. Koska vektoreita
muodostavat aina kannan. Koska vektoreita 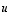 ja
ja 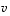 on kaksi ja tason dimensio on myös kaksi, riittää osoittaa, että ne ovat lineaarisesti riippumattomat:
on kaksi ja tason dimensio on myös kaksi, riittää osoittaa, että ne ovat lineaarisesti riippumattomat:
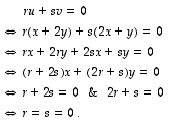
Tässä päättelyssä käytettiin olennaisesti hyväksi sitä tietoa, että kantavektoreina vektorit 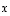 ja
ja 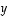 ovat lineaarisesti riippumattomia ja siten niiden lineaarikombinaatio on nolla vain, jos niiden kertoimet ovat molemmat nollia. Yllä tätä sovellettiin kertoimiin
ovat lineaarisesti riippumattomia ja siten niiden lineaarikombinaatio on nolla vain, jos niiden kertoimet ovat molemmat nollia. Yllä tätä sovellettiin kertoimiin 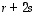 ja
ja 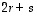 .
Tuloksen mukaan vektorit
.
Tuloksen mukaan vektorit 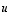 ja
ja 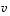 ovat lineaarisesti riippumattomat ja muodostavat tason kannan.
ovat lineaarisesti riippumattomat ja muodostavat tason kannan.
(b) Tarkastellaan sitten vektoria 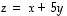 .
Sen koordinaatit kannassa
.
Sen koordinaatit kannassa 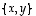 ovat tietenkin 1 ja 5. Mutta mitkä sen koordinaatit ovat kannassa
ovat tietenkin 1 ja 5. Mutta mitkä sen koordinaatit ovat kannassa 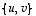 ? Ratkaistaan nämä, olkoot ne
? Ratkaistaan nämä, olkoot ne 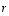 ja
ja 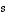 ,
seuraavasti:
,
seuraavasti:
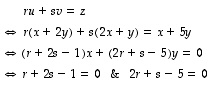
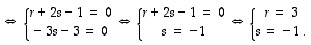
Kysytyt koordinaatit ovat siis 3 ja -1 ja vektorilla 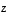 on sen mukaan esitys
on sen mukaan esitys 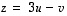 .
.
(c) Konkreettina esimerkkinä tilanne on alla olevassa kuvassa erikseen kuvattu tason vektoreille 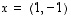 ja
ja 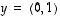 .
Etsi kuvasta kaikki yllä mainitut koordinaattivektorit ja tarkista niiden toimivuus!
.
Etsi kuvasta kaikki yllä mainitut koordinaattivektorit ja tarkista niiden toimivuus!

Yllä oleva esimerkki osoittaa, että eri kannoissa koordinaatit voivat muuttua hyvinkin paljon ja että niiden määräämiseksi joudutaan jo kaksiulotteisessa tapauksessa tekemään jonkun verran työtä eikä tuloskaan näytä mitenkään helposti olevan ennakoitavissa. Myöhemmin, lineaarikuvausten ja matriisien käsittelyn jälkeen luvussa 9, johdetaan koordinaattien riippuvuuksille kuitenkin selkeämpiä sääntöjä.
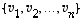 on avaruuden
on avaruuden 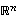 kanta, kukin vektori
kanta, kukin vektori 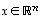 voidaan esittää yksikäsitteisesti niiden lineaarikombinaationa eli muodossa
voidaan esittää yksikäsitteisesti niiden lineaarikombinaationa eli muodossa 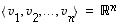 ,
kyseisiä esityksiä on aina olemassa. Olkoon sitten vektorilla
,
kyseisiä esityksiä on aina olemassa. Olkoon sitten vektorilla 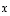 myös toinen esitys
myös toinen esitys 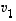 ,
,
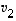 ,
...,
,
..., 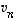 ovat lineaarisesti riippumattomat, yllä saadussa yhtälössä niiden kertoimet ovat kaikki nollia. Siten
ovat lineaarisesti riippumattomat, yllä saadussa yhtälössä niiden kertoimet ovat kaikki nollia. Siten 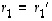 ,
,
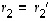 ,
...,
,
..., 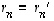 .
Vektorin
.
Vektorin 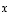 esitykset ovat näin ollen samat.
esitykset ovat näin ollen samat. 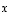 koordinaattiesitys kannassa
koordinaattiesitys kannassa 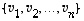 ja luvut
ja luvut 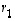 ,
,
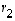 ,
...,
,
..., 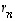 ovat sen
koordinaatit tässä kannassa.
ovat sen
koordinaatit tässä kannassa. 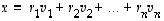 .
.
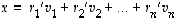 .
.
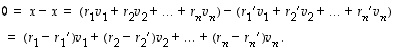

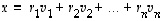
 on jokin - mikä tahansa - tason kanta.
on jokin - mikä tahansa - tason kanta. 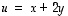 ja
ja 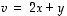 muodostavat aina kannan. Koska vektoreita
muodostavat aina kannan. Koska vektoreita 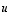 ja
ja 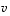 on kaksi ja tason dimensio on myös kaksi, riittää osoittaa, että ne ovat lineaarisesti riippumattomat:
on kaksi ja tason dimensio on myös kaksi, riittää osoittaa, että ne ovat lineaarisesti riippumattomat: 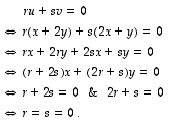
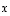 ja
ja 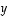 ovat lineaarisesti riippumattomia ja siten niiden lineaarikombinaatio on nolla vain, jos niiden kertoimet ovat molemmat nollia. Yllä tätä sovellettiin kertoimiin
ovat lineaarisesti riippumattomia ja siten niiden lineaarikombinaatio on nolla vain, jos niiden kertoimet ovat molemmat nollia. Yllä tätä sovellettiin kertoimiin 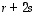 ja
ja 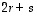 .
Tuloksen mukaan vektorit
.
Tuloksen mukaan vektorit 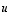 ja
ja 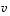 ovat lineaarisesti riippumattomat ja muodostavat tason kannan.
ovat lineaarisesti riippumattomat ja muodostavat tason kannan. 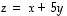 .
Sen koordinaatit kannassa
.
Sen koordinaatit kannassa 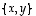 ovat tietenkin 1 ja 5. Mutta mitkä sen koordinaatit ovat kannassa
ovat tietenkin 1 ja 5. Mutta mitkä sen koordinaatit ovat kannassa 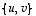 ? Ratkaistaan nämä, olkoot ne
? Ratkaistaan nämä, olkoot ne 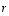 ja
ja 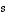 ,
seuraavasti:
,
seuraavasti: 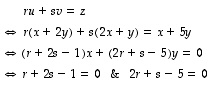
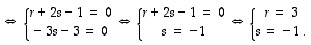
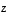 on sen mukaan esitys
on sen mukaan esitys 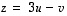 .
.
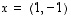 ja
ja 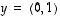 .
Etsi kuvasta kaikki yllä mainitut koordinaattivektorit ja tarkista niiden toimivuus!
.
Etsi kuvasta kaikki yllä mainitut koordinaattivektorit ja tarkista niiden toimivuus! 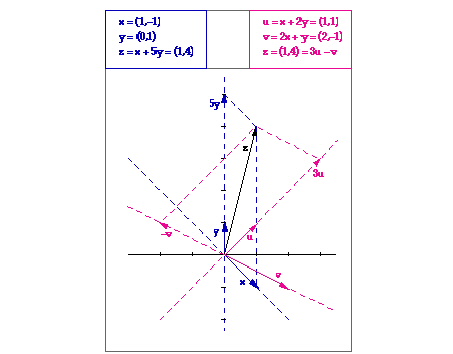

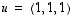 ,
,
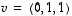 ja
ja 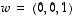 muodostavat avaruuden
muodostavat avaruuden 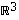 kannan.
kannan. 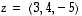 koordinaatit tässä kannassa
koordinaatit tässä kannassa