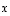 ,
,
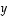 ja
ja 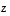 ,
jotka ovat lineaarisesti riippuvat, mutta joista
,
jotka ovat lineaarisesti riippuvat, mutta joista 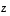 ei ole vektorien
ei ole vektorien 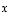 ja
ja 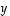 lineaarikombinaatio.
lineaarikombinaatio.
1. Keksi esimerkkejä sellaisista vektoreista 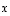 ,
,
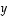 ja
ja 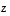 ,
jotka ovat lineaarisesti riippuvat, mutta joista
,
jotka ovat lineaarisesti riippuvat, mutta joista 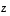 ei ole vektorien
ei ole vektorien 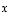 ja
ja 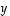 lineaarikombinaatio.
lineaarikombinaatio.
2. Tarkastele vektoreita 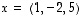 ,
,
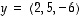 ja
ja 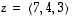 .
Osoita, että näistä vektori
.
Osoita, että näistä vektori 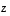 voidaan esittää muiden vektoreiden (eli nyt siis vektoreiden
voidaan esittää muiden vektoreiden (eli nyt siis vektoreiden 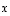 ja
ja 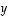 ) lineaarikombinaationa. Voidaanko sama tehdä vektorille
) lineaarikombinaationa. Voidaanko sama tehdä vektorille 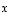 tai vektorille
tai vektorille 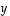 ?
?
3. (a) Ovatko vektorit 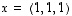 ,
,
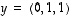 ja
ja 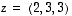 lineaarisesti riippumattomat?
lineaarisesti riippumattomat?
(b) Esitä vektori 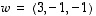 ainakin kolmella eri tavalla vektoreiden
ainakin kolmella eri tavalla vektoreiden 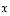 ,
,
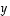 ja
ja 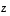 lineaarikombinaationa. Miksi tämä on mahdollista?
lineaarikombinaationa. Miksi tämä on mahdollista?
4. Osoita, että vektorit 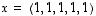 ,
,
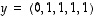 ,
,
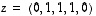 ja
ja 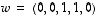 ovat lineaarisesti riippumattomat. Voitko lisätä listaan vielä yhden vektorin niin, että koko vektorijoukko pysyy lineaarisesti riippumattomana?
ovat lineaarisesti riippumattomat. Voitko lisätä listaan vielä yhden vektorin niin, että koko vektorijoukko pysyy lineaarisesti riippumattomana?
5. (a) Olkoot kolmion 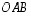 kärkinä origo
kärkinä origo 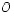 ja lineaarisesti riippumattomien vektoreiden
ja lineaarisesti riippumattomien vektoreiden 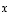 ja
ja 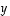 päätepisteet
päätepisteet 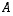 ja
ja 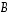 .
Lausu kolmion
.
Lausu kolmion 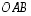 kaikki mediaanit (eli kärjen ja vastakkaisen sivun keskipisteen yhdistävät janat) vektoreiden
kaikki mediaanit (eli kärjen ja vastakkaisen sivun keskipisteen yhdistävät janat) vektoreiden 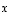 ja
ja 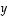 avulla.
avulla.
(b) Osoita edellisen kohdan avulla, että kolmion mediaanit leikkaavat toisensa samassa pisteessä.
6. Valittavanasi on seuraavat kuusi vektoria: 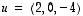 ,
,
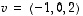 ,
,
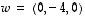 ,
,
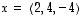 ,
,
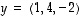 ja
ja 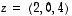 .
Valitsemalla näitä vektoreita muodosta (ilman mitään lineaarikombinaatioita) jokin avaruuden
.
Valitsemalla näitä vektoreita muodosta (ilman mitään lineaarikombinaatioita) jokin avaruuden 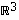 kanta ja osoita se sellaiseksi. Kokeile erilaisia valintoja.
kanta ja osoita se sellaiseksi. Kokeile erilaisia valintoja.
7. Täydennä vektorit 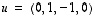 ja
ja 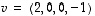 avaruuden
avaruuden 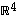 kannaksi, ts. keksi tarpeellinen määrä lisävektoreita niin, että ne yhdessä vektoreiden
kannaksi, ts. keksi tarpeellinen määrä lisävektoreita niin, että ne yhdessä vektoreiden 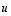 ja
ja 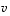 kanssa muodostavat avaruuden
kanssa muodostavat avaruuden 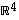 kannan. Perustele mahdollisimman lyhyesti valintasi. Mieti myös, oletko löytänyt 'helpoimman' valinnan.
kannan. Perustele mahdollisimman lyhyesti valintasi. Mieti myös, oletko löytänyt 'helpoimman' valinnan.