Implisiittifunktio
Jatkuvan reaalifunktion 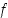 kuvaaja on käyrä, joka muodostuu niistä tason pisteistä
kuvaaja on käyrä, joka muodostuu niistä tason pisteistä 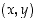 ,
joille
,
joille 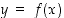 . Tason käyrämäisiä pistejoukkoja voidaan kuitenkin ilmaista muutenkin kuin funktion kuvaajana. Esimerkiksi yhtälö
. Tason käyrämäisiä pistejoukkoja voidaan kuitenkin ilmaista muutenkin kuin funktion kuvaajana. Esimerkiksi yhtälö 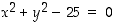 määrittelee origokeskisen ympyrän, jonka säde on 5. Näitä pisteitä ei voi esittää minkään yhden funktion kuvaajana, koska esimerkiksi arvolle
määrittelee origokeskisen ympyrän, jonka säde on 5. Näitä pisteitä ei voi esittää minkään yhden funktion kuvaajana, koska esimerkiksi arvolle 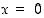 löytyy kaksi arvoa
löytyy kaksi arvoa 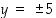 ,
jotka toteuttavat ympyrän yhtälön. Toki kyseinen ympyrä voidaan esittää kahden eri funktion kuvaajien yhdisteenä: toinen on määritelty lausekkeella
,
jotka toteuttavat ympyrän yhtälön. Toki kyseinen ympyrä voidaan esittää kahden eri funktion kuvaajien yhdisteenä: toinen on määritelty lausekkeella 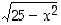 ja toinen lausekkeella
ja toinen lausekkeella 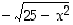 .
.
Tarkastellaan yleisesti muotoa
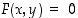
olevia kahdesta muuttujasta muodostuvia lausekkeita, jossa 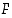 on siis kahden muuttujan funktio. Esimerkiksi edellä olevalle ympyräkaarelle on
on siis kahden muuttujan funktio. Esimerkiksi edellä olevalle ympyräkaarelle on 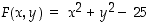 . Toisaalta annetulle funktiolle
. Toisaalta annetulle funktiolle 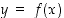 lauseke
lauseke 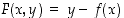 toteuttaa ehdon
toteuttaa ehdon 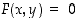 funktion
funktion 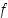 kuvaajan pisteissä. Yleisesti sanotaan, että ehto
kuvaajan pisteissä. Yleisesti sanotaan, että ehto 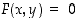 määrittelee tasokäyrän, kun funktio
määrittelee tasokäyrän, kun funktio 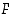 on jatkuva. Se, mitä kahden muuttujan funktion jatkuvuudella tarkoitetaan, on kuitenkin mahdollista selvittää vasta usean muuttujan analyysin yhteydessä. Funktion
on jatkuva. Se, mitä kahden muuttujan funktion jatkuvuudella tarkoitetaan, on kuitenkin mahdollista selvittää vasta usean muuttujan analyysin yhteydessä. Funktion 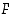 muodosta ja säännöllisyydestä riippuu kuitenkin, kuinka säännöllinen käyrä ehdosta
muodosta ja säännöllisyydestä riippuu kuitenkin, kuinka säännöllinen käyrä ehdosta 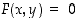 määräytyy, jos ylipäätään ehdon toteuttavat pisteet liittyvät toisiinsa edes "käyrämäisesti" eli jatkuvasti ja "ohuesti". Välttämättä ei ole edes yhtään annetun ehdon toteuttavaa pistettä olemassa, kuten yhtälön
määräytyy, jos ylipäätään ehdon toteuttavat pisteet liittyvät toisiinsa edes "käyrämäisesti" eli jatkuvasti ja "ohuesti". Välttämättä ei ole edes yhtään annetun ehdon toteuttavaa pistettä olemassa, kuten yhtälön 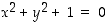 tapauksessa.
tapauksessa.
Tässä pykälässä oletamme, että ehto 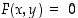 määrittelee tarkasteltavan pisteen
määrittelee tarkasteltavan pisteen 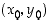 lähistöllä jonkin funktion
lähistöllä jonkin funktion 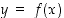 kuvaajan. Tarkemmin sanottuna tämä tarkoittaa sitä, että on olemassa jokin pisteen
kuvaajan. Tarkemmin sanottuna tämä tarkoittaa sitä, että on olemassa jokin pisteen 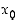 sisältävä väli ja sillä määritelty funktio
sisältävä väli ja sillä määritelty funktio 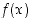 niin, että kyseisellä välillä pisteet
niin, että kyseisellä välillä pisteet 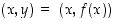 ,
ja siten myös piste
,
ja siten myös piste 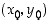 ,
toteuttavat ehdon
,
toteuttavat ehdon 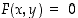 . Tällaisessa tapauksessa sanomme, että ehto
. Tällaisessa tapauksessa sanomme, että ehto 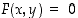 määrittelee implisiittisesti eli ratkaisemattomasti funktion
määrittelee implisiittisesti eli ratkaisemattomasti funktion 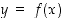 . Jos tämä funktio ja varsinkin jos sen lauseke pystytään ratkaisemaan, antaa se eksplisiittisen eli ratkaistun muodon funktiolle.
. Jos tämä funktio ja varsinkin jos sen lauseke pystytään ratkaisemaan, antaa se eksplisiittisen eli ratkaistun muodon funktiolle.
Esimerkki 3.4.4.
Tarkastellaan yhtälöä 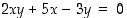 . Tästä saadaan muuttuja
. Tästä saadaan muuttuja 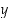 ratkaistua muodossa
ratkaistua muodossa
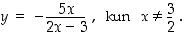
Siten annettu yhtälö määrittelee implisiittisesti funktion 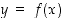 ,
jonka eksplisiittinen muoto on edellä ratkaistu muoto. Huomaa, että ratkaisufunktiota ei ole määritelty yhdessä pisteessä, mitä ei välttämättä huomaa implisiittisestä ehdosta.
,
jonka eksplisiittinen muoto on edellä ratkaistu muoto. Huomaa, että ratkaisufunktiota ei ole määritelty yhdessä pisteessä, mitä ei välttämättä huomaa implisiittisestä ehdosta.

Esimerkki 3.4.5.
Yhtälöstä 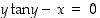 ei muuttujaa
ei muuttujaa 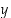 voida ratkaista muodossa
voida ratkaista muodossa 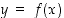 eli tätä yhtälöä ei voida eksplisiittisesti ratkaista. Voidaan kuitenkin osoittaa, että sillä on esimerkiksi olemassa eräs ratkaisufunktio, jonka kuvaaja kulkee pisteen
eli tätä yhtälöä ei voida eksplisiittisesti ratkaista. Voidaan kuitenkin osoittaa, että sillä on esimerkiksi olemassa eräs ratkaisufunktio, jonka kuvaaja kulkee pisteen 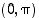 kautta.
kautta.

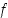 kuvaaja on käyrä, joka muodostuu niistä tason pisteistä
kuvaaja on käyrä, joka muodostuu niistä tason pisteistä 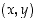 ,
joille
,
joille 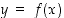 . Tason käyrämäisiä pistejoukkoja voidaan kuitenkin ilmaista muutenkin kuin funktion kuvaajana. Esimerkiksi yhtälö
. Tason käyrämäisiä pistejoukkoja voidaan kuitenkin ilmaista muutenkin kuin funktion kuvaajana. Esimerkiksi yhtälö 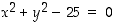 määrittelee origokeskisen ympyrän, jonka säde on 5. Näitä pisteitä ei voi esittää minkään yhden funktion kuvaajana, koska esimerkiksi arvolle
määrittelee origokeskisen ympyrän, jonka säde on 5. Näitä pisteitä ei voi esittää minkään yhden funktion kuvaajana, koska esimerkiksi arvolle 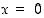 löytyy kaksi arvoa
löytyy kaksi arvoa 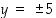 ,
jotka toteuttavat ympyrän yhtälön. Toki kyseinen ympyrä voidaan esittää kahden eri funktion kuvaajien yhdisteenä: toinen on määritelty lausekkeella
,
jotka toteuttavat ympyrän yhtälön. Toki kyseinen ympyrä voidaan esittää kahden eri funktion kuvaajien yhdisteenä: toinen on määritelty lausekkeella 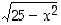 ja toinen lausekkeella
ja toinen lausekkeella 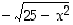 .
. 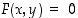
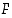 on siis kahden muuttujan funktio. Esimerkiksi edellä olevalle ympyräkaarelle on
on siis kahden muuttujan funktio. Esimerkiksi edellä olevalle ympyräkaarelle on 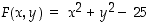 . Toisaalta annetulle funktiolle
. Toisaalta annetulle funktiolle 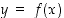 lauseke
lauseke 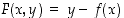 toteuttaa ehdon
toteuttaa ehdon 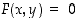 funktion
funktion 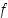 kuvaajan pisteissä. Yleisesti sanotaan, että ehto
kuvaajan pisteissä. Yleisesti sanotaan, että ehto 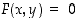 määrittelee tasokäyrän
määrittelee tasokäyrän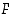 on jatkuva. Se, mitä kahden muuttujan funktion jatkuvuudella tarkoitetaan, on kuitenkin mahdollista selvittää vasta usean muuttujan analyysin yhteydessä. Funktion
on jatkuva. Se, mitä kahden muuttujan funktion jatkuvuudella tarkoitetaan, on kuitenkin mahdollista selvittää vasta usean muuttujan analyysin yhteydessä. Funktion 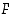 muodosta ja säännöllisyydestä riippuu kuitenkin, kuinka säännöllinen käyrä ehdosta
muodosta ja säännöllisyydestä riippuu kuitenkin, kuinka säännöllinen käyrä ehdosta 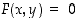 määräytyy, jos ylipäätään ehdon toteuttavat pisteet liittyvät toisiinsa edes "käyrämäisesti" eli jatkuvasti ja "ohuesti". Välttämättä ei ole edes yhtään annetun ehdon toteuttavaa pistettä olemassa, kuten yhtälön
määräytyy, jos ylipäätään ehdon toteuttavat pisteet liittyvät toisiinsa edes "käyrämäisesti" eli jatkuvasti ja "ohuesti". Välttämättä ei ole edes yhtään annetun ehdon toteuttavaa pistettä olemassa, kuten yhtälön 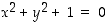 tapauksessa.
tapauksessa. 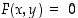 määrittelee tarkasteltavan pisteen
määrittelee tarkasteltavan pisteen 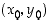 lähistöllä jonkin funktion
lähistöllä jonkin funktion 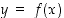 kuvaajan. Tarkemmin sanottuna tämä tarkoittaa sitä, että on olemassa jokin pisteen
kuvaajan. Tarkemmin sanottuna tämä tarkoittaa sitä, että on olemassa jokin pisteen 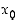 sisältävä väli ja sillä määritelty funktio
sisältävä väli ja sillä määritelty funktio 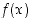 niin, että kyseisellä välillä pisteet
niin, että kyseisellä välillä pisteet 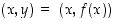 ,
ja siten myös piste
,
ja siten myös piste 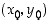 ,
toteuttavat ehdon
,
toteuttavat ehdon 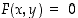 . Tällaisessa tapauksessa sanomme, että ehto
. Tällaisessa tapauksessa sanomme, että ehto 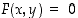 määrittelee implisiittisesti
määrittelee implisiittisesti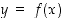 . Jos tämä funktio ja varsinkin jos sen lauseke pystytään ratkaisemaan, antaa se eksplisiittisen
. Jos tämä funktio ja varsinkin jos sen lauseke pystytään ratkaisemaan, antaa se eksplisiittisen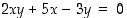 . Tästä saadaan muuttuja
. Tästä saadaan muuttuja 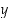 ratkaistua muodossa
ratkaistua muodossa 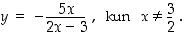
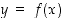 ,
jonka eksplisiittinen muoto on edellä ratkaistu muoto. Huomaa, että ratkaisufunktiota ei ole määritelty yhdessä pisteessä, mitä ei välttämättä huomaa implisiittisestä ehdosta.
,
jonka eksplisiittinen muoto on edellä ratkaistu muoto. Huomaa, että ratkaisufunktiota ei ole määritelty yhdessä pisteessä, mitä ei välttämättä huomaa implisiittisestä ehdosta. 
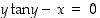 ei muuttujaa
ei muuttujaa 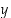 voida ratkaista muodossa
voida ratkaista muodossa 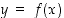 eli tätä yhtälöä ei voida eksplisiittisesti ratkaista. Voidaan kuitenkin osoittaa, että sillä on esimerkiksi olemassa eräs ratkaisufunktio, jonka kuvaaja kulkee pisteen
eli tätä yhtälöä ei voida eksplisiittisesti ratkaista. Voidaan kuitenkin osoittaa, että sillä on esimerkiksi olemassa eräs ratkaisufunktio, jonka kuvaaja kulkee pisteen 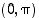 kautta.
kautta. 