Korkeammat derivaatat
Jollain välillä derivoituvan funktion 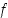 derivaatta on sillä välillä määritelty funktio
derivaatta on sillä välillä määritelty funktio 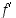 . Sen derivoituvuutta voidaan siten edelleen selvittää. Jos
. Sen derivoituvuutta voidaan siten edelleen selvittää. Jos 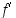 on derivoituva, on sen derivaatta
on derivoituva, on sen derivaatta 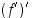 alkuperäisen funktion
alkuperäisen funktion 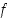 toinen derivaatta (tai toisen kertaluvun derivaatta) ja sitä merkitään
toinen derivaatta (tai toisen kertaluvun derivaatta) ja sitä merkitään 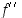 tai
tai 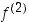 .
.
Vastaavasti kolmas derivaatta 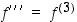 on toisen derivaatan derivaatta, mikäli sellainen on olemassa.
on toisen derivaatan derivaatta, mikäli sellainen on olemassa.
Esimerkki 3.4.1.
Polynomifunktion 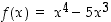 derivaatta
derivaatta 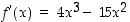 on polynomina derivoituva, joten toinen derivaatta on olemassa ja
on polynomina derivoituva, joten toinen derivaatta on olemassa ja 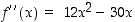 .
.
Edelleen kolmas derivaatta on 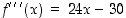 .
.

Yleisesti positiiviselle kokonaisluvulle 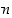 määritellään induktiivisesti, että funktion
määritellään induktiivisesti, että funktion 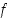
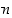 :s derivaatta (eli
:s derivaatta (eli 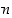 :n kertaluvun derivaatta)
:n kertaluvun derivaatta) 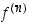 on edellisen kertaluvun derivaatan
on edellisen kertaluvun derivaatan 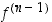 derivaatta, mikäli se (ja jokainen edeltävä derivaatta) on olemassa. Induktiivisen määrittelyn aloitukseksi sovitaan, että nollas derivaatta
derivaatta, mikäli se (ja jokainen edeltävä derivaatta) on olemassa. Induktiivisen määrittelyn aloitukseksi sovitaan, että nollas derivaatta 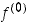 tarkoittaa itse funktiota eli
tarkoittaa itse funktiota eli 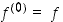 . Derivaatoista
. Derivaatoista 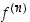 käytetään myös merkintöjä
käytetään myös merkintöjä

Jos funktiolla 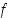 on
on 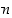 :s derivaatta jollain välillä, sanotaan myös, että
:s derivaatta jollain välillä, sanotaan myös, että 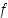 on
on 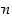 kertaa derivoituva kyseisellä välillä.
kertaa derivoituva kyseisellä välillä.
Esimerkki 3.4.2.
Funktiolle 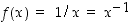 (missä
(missä 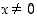 ) on
) on
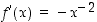 ,
,
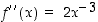 ,
,
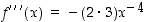 ,
,
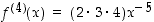 ,
...
,
...
ja yleisesti kertaluvulle 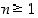 on
on
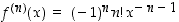 ,
,
missä 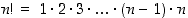 on
on 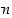 −kertoma. (Tarkka todistus tehdään induktiolla, mutta se sivuutetaan tässä.)
−kertoma. (Tarkka todistus tehdään induktiolla, mutta se sivuutetaan tässä.)

Esimerkki 3.4.3.
Funktiolle 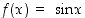 on
on
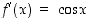 ,
,
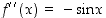 ,
,
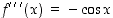 ,
,
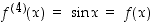 ,
,
ja siten yleisesti kokonaisluvulle 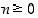 on
on
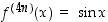 ,
,
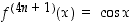 ,
,
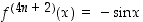 ,
,
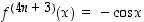 .
.

Edellä olevien esimerkkien funktioilla on siis kaikkien kertalukujen derivaatat olemassa. Sanotaan, että ne ovat äärettömän monta kertaa derivoituvat. Kaikki polynomit ja rationaalifunktiot ovat äärettömän monta kertaa derivoituvia funktioita (polynomit kaikkialla ja rationaalifunktiot määrittelyväleillään).
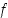 derivaatta on sillä välillä määritelty funktio
derivaatta on sillä välillä määritelty funktio 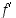 . Sen derivoituvuutta voidaan siten edelleen selvittää. Jos
. Sen derivoituvuutta voidaan siten edelleen selvittää. Jos 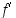 on derivoituva, on sen derivaatta
on derivoituva, on sen derivaatta 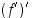 alkuperäisen funktion
alkuperäisen funktion 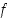 toinen derivaatta (tai toisen kertaluvun derivaatta) ja sitä merkitään
toinen derivaatta (tai toisen kertaluvun derivaatta) ja sitä merkitään 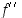 tai
tai 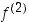 .
. 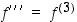 on toisen derivaatan derivaatta, mikäli sellainen on olemassa.
on toisen derivaatan derivaatta, mikäli sellainen on olemassa. 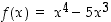 derivaatta
derivaatta 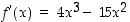 on polynomina derivoituva, joten toinen derivaatta on olemassa ja
on polynomina derivoituva, joten toinen derivaatta on olemassa ja 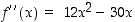 .
. 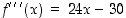 .
. 
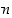 määritellään induktiivisesti, että funktion
määritellään induktiivisesti, että funktion 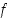
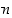 :s derivaatta (eli
:s derivaatta (eli 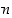 :n kertaluvun
:n kertaluvun 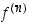 on edellisen kertaluvun derivaatan
on edellisen kertaluvun derivaatan 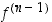 derivaatta, mikäli se (ja jokainen edeltävä derivaatta) on olemassa. Induktiivisen määrittelyn aloitukseksi sovitaan, että nollas derivaatta
derivaatta, mikäli se (ja jokainen edeltävä derivaatta) on olemassa. Induktiivisen määrittelyn aloitukseksi sovitaan, että nollas derivaatta 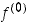 tarkoittaa itse funktiota eli
tarkoittaa itse funktiota eli 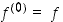 . Derivaatoista
. Derivaatoista 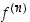 käytetään myös merkintöjä
käytetään myös merkintöjä 
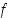 on
on 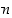 :s derivaatta jollain välillä, sanotaan myös, että
:s derivaatta jollain välillä, sanotaan myös, että 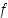 on
on 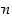 kertaa derivoituva kyseisellä välillä.
kertaa derivoituva kyseisellä välillä. 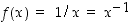 (missä
(missä 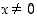 ) on
) on 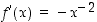 ,
,
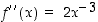 ,
,
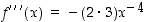 ,
,
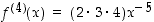 ,
...
,
... 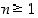 on
on 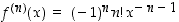 ,
,
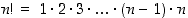 on
on 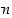 −kertoma
−kertoma
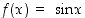 on
on 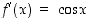 ,
,
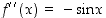 ,
,
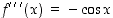 ,
,
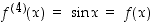 ,
,
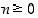 on
on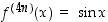 ,
,
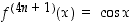 ,
,
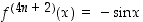 ,
,
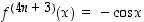 .
. 