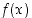 on op. raja-arvo
on op. raja-arvo 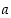 pisteessä
pisteessä 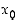 täsmälleen silloin, kun
täsmälleen silloin, kun 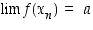 kaikille jonoille
kaikille jonoille 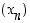 ,
joille
,
joille 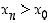 ja
ja 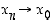 . Vastaava pätee vp. raja-arvolle.
. Vastaava pätee vp. raja-arvolle.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Funktion raja-arvoja voidaan selvittää myös jonojen avulla. Todetaan ensin seuraava tulos.
Lause 2.2.16. (Raja-arvon jonokarakterisointi)
Funktiolla 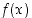 on op. raja-arvo
on op. raja-arvo 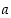 pisteessä
pisteessä 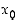 täsmälleen silloin, kun
täsmälleen silloin, kun 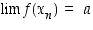 kaikille jonoille
kaikille jonoille 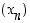 ,
joille
,
joille 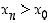 ja
ja 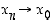 . Vastaava pätee vp. raja-arvolle.
. Vastaava pätee vp. raja-arvolle.
Todistus. Op. raja-arvon olemassaolosta seuraa suoraan määritelmän perusteella kuvattu jono-ominaisuus.
Oletetaan sitten, että funktiolla 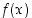 ei ole op. raja-arvonaan lukua
ei ole op. raja-arvonaan lukua 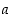 pisteessä
pisteessä 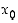 . Silloin on olemassa jokin sellainen luku
. Silloin on olemassa jokin sellainen luku 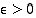 ,
jolle jokaiselle
,
jolle jokaiselle 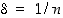 on olemassa sellainen piste
on olemassa sellainen piste 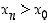 ,
että
,
että 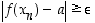 vaikka
vaikka 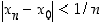 . Tällä tavalla saadaan muodostettua jono
. Tällä tavalla saadaan muodostettua jono 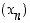 ,
joka suppenee kohti pistettä
,
joka suppenee kohti pistettä 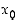 ,
mutta jonka arvot
,
mutta jonka arvot 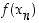 eivät suppene kohti arvoa
eivät suppene kohti arvoa 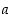 . Näin on saatu aikaan päättely, joka osoittaa, että funktiolla
. Näin on saatu aikaan päättely, joka osoittaa, että funktiolla 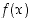 on oltava op. raja-arvo, mikäli oletetaan, että kaikki kohti pistettä
on oltava op. raja-arvo, mikäli oletetaan, että kaikki kohti pistettä 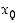 suppenevien jonojen kuvajonot
suppenevien jonojen kuvajonot 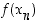 suppenevat kohti arvoa
suppenevat kohti arvoa 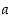 .
.
Edellä olevaa lausetta voidaan käyttää raja-arvojen etsimiseen. Jos esimerkiksi löydetään jokin pistettä 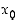 kohti suppeneva jono
kohti suppeneva jono 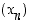 ,
jolle myös arvot
,
jolle myös arvot 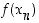 suppenevat, on tämän jonon raja-arvo ainoa ehdokas itse funktionkin raja-arvoksi. Tämä ei kuitenkaan vielä osoita kyseistä lukua raja-arvoksi, vaan se on erikseen yleispätevällä tavalla todistettava. Toisaalta on mahdollista, että löytyy jokin toinen pistettä
suppenevat, on tämän jonon raja-arvo ainoa ehdokas itse funktionkin raja-arvoksi. Tämä ei kuitenkaan vielä osoita kyseistä lukua raja-arvoksi, vaan se on erikseen yleispätevällä tavalla todistettava. Toisaalta on mahdollista, että löytyy jokin toinen pistettä 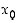 kohti suppeneva jono
kohti suppeneva jono 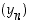 ,
jolle arvot
,
jolle arvot 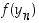 eivät suppene tai suppenevat kohti toista lukua. Tämä osoittaa silloin, että funktiolla ei ole raja-arvoa tarkastelupisteessä.
eivät suppene tai suppenevat kohti toista lukua. Tämä osoittaa silloin, että funktiolla ei ole raja-arvoa tarkastelupisteessä.
On varsin ilmeistä, että raja-arvoa
ei ole olemassa. Perustellaan se. Etsitään sitä varten nollaan suppenevia jonoja, joiden kuvajonot antavat erilaisia raja-arvoja. Koska
Valitaan tämän mukaisesti jonot 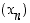 ja
ja 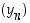 seuraavasti:
seuraavasti:
Silloin 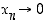 ja
ja 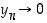 . Toisaalta valinnastamme johtuen
. Toisaalta valinnastamme johtuen
kaikilla 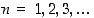 ,
joten näiden vakiojonojen raja-arvotkin ovat +1 ja −1 vastaavasti. Niinpä, jos funktiolla
,
joten näiden vakiojonojen raja-arvotkin ovat +1 ja −1 vastaavasti. Niinpä, jos funktiolla 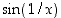 olisi op. raja-arvo nollassa, olisi sen oltava toisaalta +1 ja toisaalta −1. Kyseistä raja-arvoa ei siten ole olemassa. Vastaavasta syystä myöskään vp. raja-arvoa ei ole olemassa.
olisi op. raja-arvo nollassa, olisi sen oltava toisaalta +1 ja toisaalta −1. Kyseistä raja-arvoa ei siten ole olemassa. Vastaavasta syystä myöskään vp. raja-arvoa ei ole olemassa.