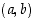 sekä sitä kulmaa
sekä sitä kulmaa 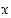 , joka muodostuu origosta pisteeseen
, joka muodostuu origosta pisteeseen 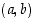 menevän säteen ja vaaka-akselin väliin (ks. kuva 17).
menevän säteen ja vaaka-akselin väliin (ks. kuva 17).
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan tasossa origokeskisen yksikköympyrän pistettä 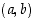 sekä sitä kulmaa
sekä sitä kulmaa 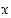 , joka muodostuu origosta pisteeseen
, joka muodostuu origosta pisteeseen 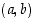 menevän säteen ja vaaka-akselin väliin (ks. kuva 17).
menevän säteen ja vaaka-akselin väliin (ks. kuva 17).
Kulma mitataan yleensä vaaka-akselista vastapäivään (eli positiiviseen suuntaan) laskettuna niin, että oikokulma on 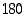 astetta (º) eli
astetta (º) eli 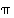 radiaania (rad). Täysi kulma on siten
radiaania (rad). Täysi kulma on siten 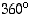 eli
eli 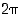 radiaania ja suora kulma on
radiaania ja suora kulma on 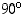 eli
eli 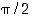 radiaania. Siten
radiaania. Siten
Koska yksikköympyrän kaaren pituus on 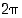 ,
on kulman suuruus radiaaneissa ilmoitettuna samalla sitä vastaavan yksikköympyrän kaaren pituus. Mm. tästä syystä laskuissa on hyvä käyttää radiaania kulmayksikkönä. Vastakkaiseen suuntaan eli myötäpäivään mitattuna kulma saa vastaavansuuruisen negatiivisen arvon.
,
on kulman suuruus radiaaneissa ilmoitettuna samalla sitä vastaavan yksikköympyrän kaaren pituus. Mm. tästä syystä laskuissa on hyvä käyttää radiaania kulmayksikkönä. Vastakkaiseen suuntaan eli myötäpäivään mitattuna kulma saa vastaavansuuruisen negatiivisen arvon.
Yksikköympyrän pisteen 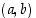 koordinaattien avulla määritellään kulman
koordinaattien avulla määritellään kulman 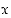 trigonometriset funktiot sini, kosini, tangentti ja kotangentti seuraavasti:
trigonometriset funktiot sini, kosini, tangentti ja kotangentti seuraavasti:
Huomaa, että tässä 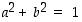 ,
koska piste
,
koska piste 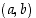 on yksikköympyrällä.
on yksikköympyrällä.
Havainnollistus: Sini ja kosini 
Trigonometrisistä funktioista sini ja kosini tulevat kaikkialla määritellyiksi. Tangentti ja kotangentti ovat taas määriteltyjä vain silloin, kun niiden lausekkeiden nimittäjät − kosini ja sini vastaavasti − ovat nollasta eroavat. Kyseisten funktioiden nollakohdat toistuvat:
Trigonometristen funktioiden määrittelyjoukot ovat siten seuraavat:
Trigonometristen funktioiden arvojoukot ovat
Trigonometrisistä funktioista kosini on parillinen, ts. 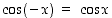 ,
ja muut kolme ovat parittomia, ts. ne toteuttavat ehdon
,
ja muut kolme ovat parittomia, ts. ne toteuttavat ehdon 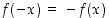 kaikissa määrittelypisteissään.
kaikissa määrittelypisteissään.
Kaikki trigonometriset funktiot ovat jaksollisia. Funktiota 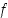 sanotaan jaksolliseksi, jos sille pätee määrittelyjoukossaan, että
sanotaan jaksolliseksi, jos sille pätee määrittelyjoukossaan, että 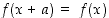 jollekin nollasta eroavalle vakiolle
jollekin nollasta eroavalle vakiolle 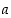 . Pienintä tällaista positiivista vakiota
. Pienintä tällaista positiivista vakiota 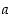 sanotaan funktion
sanotaan funktion 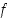 (perus)jaksoksi. Sinin ja kosinin jakso on
(perus)jaksoksi. Sinin ja kosinin jakso on 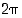 sekä tangentin ja kotangentin jakso on
sekä tangentin ja kotangentin jakso on 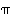 . Esimerkiksi siis
. Esimerkiksi siis  kaikilla
kaikilla 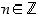 .
.
Huomautettakoon tässä siitä, että nyt annetut trigonometristen funktioiden määrittelyt ovat täysin geometrisia, eivätkä ne anna lausekkeita niille eli ne eivät ilmaise sitä, miten määrittelyissä käytetyt luvut 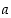 ja
ja 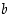 riippuvat luvusta
riippuvat luvusta 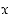 . Tällaiset lausekkeet pystytään esittämään vasta sarjateoriassa.
. Tällaiset lausekkeet pystytään esittämään vasta sarjateoriassa.
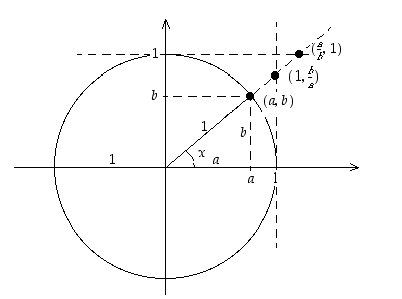
Yksikköympyrän piste 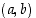 voidaan edellä olevan määrittelyn mukaan ilmoittaa keskuskulman avulla koordinaatein
voidaan edellä olevan määrittelyn mukaan ilmoittaa keskuskulman avulla koordinaatein 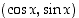 . Kääntäen kosinin ja sinin arvot löytyvät siis kulmaa vastaavan yksikköympyrän pisteen koordinaatteina. Tangentin arvo taas löytyy
. Kääntäen kosinin ja sinin arvot löytyvät siis kulmaa vastaavan yksikköympyrän pisteen koordinaatteina. Tangentin arvo taas löytyy 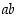 −tasossa origosta pisteeseen
−tasossa origosta pisteeseen 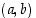 menevän säteen jatkeen ja suoran
menevän säteen jatkeen ja suoran 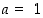 leikkauspisteen pystykoordinaattina ja kotangentin arvo vastaavasti saman säteen ja suoran
leikkauspisteen pystykoordinaattina ja kotangentin arvo vastaavasti saman säteen ja suoran 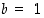 leikkauspisteen vaakakoordinaattina (ks. kuva 17).
leikkauspisteen vaakakoordinaattina (ks. kuva 17).
Kuvissa 18 ja 19 ovat trigonometristen funktioiden kuvaajat
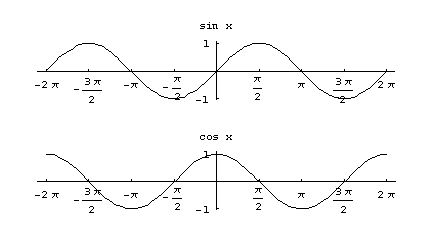
Kuva 18. Sinin ja kosinin kuvaajat.
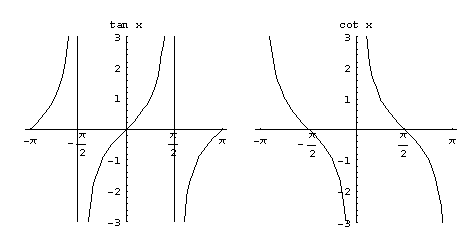
Kuva 19. Tangentin ja kotangentin kuvaajat
Suoran kulman ja sen monikertojen lisäksi kulmia 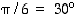 ,
,
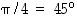 ja
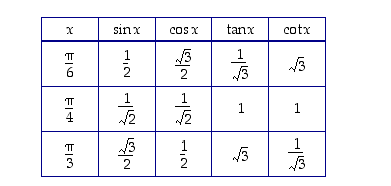
ja 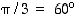 käytetään usein esimerkeissä. Niille trigonometristen funktioiden arvot ovat seuraavassa taulukossa.
käytetään usein esimerkeissä. Niille trigonometristen funktioiden arvot ovat seuraavassa taulukossa.
Opiskelutehtävä 7. (Sinin muuntaminen vakioin)
Piirrä kussakin seuraavista kohdista samaan kuvaan annettujen funktioiden kuvaajat ja määrää niiden perusjaksot.
Miten funktiot 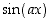 ,
,
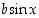 ja
ja 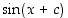 eroavat funktiosta
eroavat funktiosta 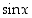 ? Entä yleisesti funktio
? Entä yleisesti funktio 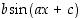 ?
?
Havainnollistus: Yksikköympyrä ja trigonometriset funktiot 
Laskentapohja: Yksikköympyrä: sini ja kosini 
Laskentapohja: Yksikköympyrä-animaatio: sini ja kosini 1 
Laskentapohja: Yksikköympyrä-animaatio: sini ja kosini 2 
Laskentapohja: Yksikköympyrä-animaatio: tangentti ja kotangentti 