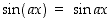 ,
kun
,
kun 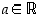 ,
ja
,
ja 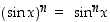 ,
kun
,
kun 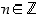 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Seuraavassa on eräitä muokkaussääntöjä sini- ja kosinifunktioille. Todistukset sivuutamme tässä. Näistä saa vastaavantapaisia sääntöjä tangentille ja kotangentille käyttämällä niiden määrittelyä sinin ja kosinin osamäärinä. Erilaisista taulukkokirjoista löytyy lisää kaavoja. Vanhaan tapaan merkitään esimerkiksi 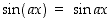 ,
kun
,
kun 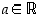 ,
ja
,
ja 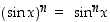 ,
kun
,
kun 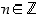 .
.
Opiskelutehtävä 8. (Sinin ja kosinin ratkaiseminen)
(b) Miten ratkaisisit yhtälön 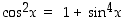 ?
?
Seuraavaa arviota tarvitsemme myöhemmin. Huomaa, että radiaaneja on käytettävä kulmayksiköinä aina, kun lausekkeissa on sekä kulmia että niistä muodostettuja (trigonometrisia) funktioita.
Kaikille reaaliluvuille on 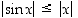 (kun kulma
(kun kulma 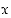 ilmoitetaan radiaaneina).
ilmoitetaan radiaaneina).
Todistus. Olkoon ensinnä 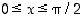 . Geometrisesti on selvää, että pisteen
. Geometrisesti on selvää, että pisteen 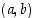 suora etäisyys vaaka-akselista eli
suora etäisyys vaaka-akselista eli 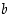 on korkeintaan se matka, joka siitä pisteestä on vaaka-akselille ympyrän kaarta pitkin (ks. kuva 17). Tämä on sama asia kuin väite.
on korkeintaan se matka, joka siitä pisteestä on vaaka-akselille ympyrän kaarta pitkin (ks. kuva 17). Tämä on sama asia kuin väite.
Olkoon sitten 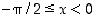 . Silloin
. Silloin 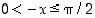 ,
joten edellisen tapauksen mukaan
,
joten edellisen tapauksen mukaan
Jäljelle jäävässä tapauksessa 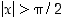 arvio on selvä:
arvio on selvä: 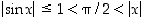 .
.