on polynomifunktiona jatkuva ja derivoituva kaikkialla. Derivaatta 
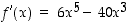on myös polynomifunktiona jatkuva ja derivoituva kaikkialla. Funktion kulun tutkimiseksi määritetään sekä ensimmäisen että toisen derivaatan nollakohdat.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Funktio on polynomifunktiona jatkuva ja derivoituva kaikkialla. Derivaatta 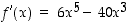on myös polynomifunktiona jatkuva ja derivoituva kaikkialla. Funktion kulun tutkimiseksi määritetään sekä ensimmäisen että toisen derivaatan nollakohdat.
joten tulon nollasäännön perusteella
mistä tulon nollasäännön perusteella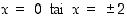 
. Saadaan merkkikaavio
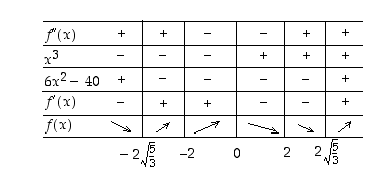
Funktio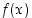 
on aidosti kasvava kun 
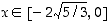tai kun 
.
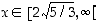Funktio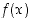 
on aidosti vähenevä kun 
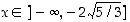tai kun 
.
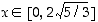Funktiolla on paikallinen maksimi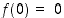 
,
paikallinen minimi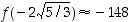 
sekä toinen paikallinen minimi 
.
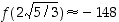Funktiolla ei ole asymptootteja, koska se on kaikilla reaaliluvuilla määritelty ja jatkuva sekä
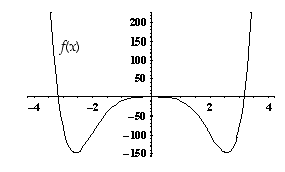
Funktiolla ei ole globaalia maksimia (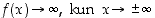
), mutta funktion lokaalit minimit ovat myös globaaleja minimejä. Kohdat 
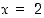ja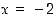 
ovat funktion käännekohtia, sillä niissä toisen derivaatan merkki vaihtuu.
[Opiskelutehtävä 30] [Vinkki tehtävään 30]
,
ja 