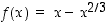on määritelty kaikilla reaaliluvuilla (murtopotenssissa neliöönkorotus suoritetaan ensin). Sen derivaatta on
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Funktio 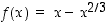on määritelty kaikilla reaaliluvuilla (murtopotenssissa neliöönkorotus suoritetaan ensin). Sen derivaatta on
Derivaatan lausekkeesta nähdään, että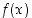 
ei ole derivoituva kun 
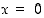. Derivaatan nollakohdat:
Laaditaan seuraavaksi kulkukaavio, johon merkitään tarkasteluvälin päätepisteet, derivaatan nollakohta sekä derivoitumattomuuskohta.
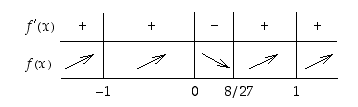
Välillä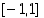 
: 
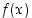on aidosti kasvava kun 
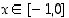tai kun 
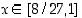ja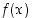 
on aidosti vähenevä kun 
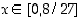. Koska
niin −2 on minimiarvo, 0 on maksimiarvo ja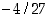 
on lokaali minimiarvo.
Yhteenveto: Funktio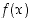 
on aidosti kasvava, kun 
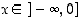tai kun 
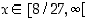. Funktio 
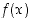on aidosti vähenevä, kun 
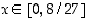. Kohdassa 
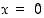funktiolla on lokaali maksimi ja kohdassa 
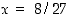lokaali minimi. Arvo 
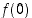ei ole globaali maksimi, sillä esim. 
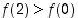. Arvo 
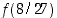ole globaali minimi, sillä esim. 
.
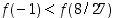[Opiskelutehtävä 28] [Vinkki tehtävään 28]
