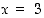täytyy tutkia erikseen. Funktio 
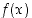on määritelty kun 
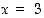ja 
.
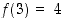[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Funktion jatkuvuus on muuten ilmeistä (molemmat lausekkeet ovat polynomifunktioina kaikkialla jatkuvia), mutta paloittain määrittelyn rajakohta 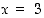täytyy tutkia erikseen. Funktio 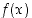on määritelty kun 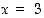ja .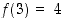
Selvitetään jatkuvuus kyseisessä kohdassa tutkimalla siinä funktion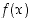 
toispuoleisia raja-arvoja:
Jotta funktiolla olisi raja-arvo kohdassa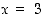 
,
toispuoleisten raja-arvojen tulee olla samat. Siten saadaan ehto:
ja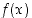 
on siis jatkuva myös kohdassa 
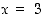. Näin ollen funktio 
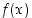on kaikkialla jatkuva, kun 
.
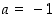[Opiskelutehtävä 14] [Vinkki tehtävään 14]
