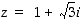 ensin moduli
ensin moduli 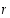 :
:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
a) Määritetään napakoordinaattiesitystä varten kompleksiluvulle 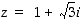 ensin moduli
ensin moduli 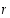 :
:
Seuraavaksi määritetään argumentti 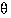 :
:
Koska kompleksiluvun 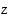 reaaliosa
reaaliosa 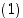 ja imaginaariosa
ja imaginaariosa 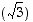 ovat molemmat positiivisia, sijaitsee
ovat molemmat positiivisia, sijaitsee 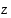 koordinaatiston ensimmäisessä neljänneksessä. Täten voidaan päätellä, että argumentti
koordinaatiston ensimmäisessä neljänneksessä. Täten voidaan päätellä, että argumentti 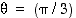 . Tällöin napakoordinaattiesityksenä
. Tällöin napakoordinaattiesityksenä
Koska kompleksiluvun 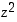 reaaliosa
reaaliosa 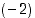 on negatiivinen ja imaginaariosa
on negatiivinen ja imaginaariosa 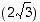 on positiivinen, niin
on positiivinen, niin 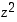 sijaitsee koordinaatiston toisessa neljänneksessä, joten
sijaitsee koordinaatiston toisessa neljänneksessä, joten 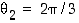 . Napakoordinaattiesityksenä
. Napakoordinaattiesityksenä
Vastaavasti voidaan laskea, että
joten 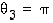 . Napakoordinaattiesityksenä
. Napakoordinaattiesityksenä 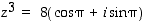 .
.
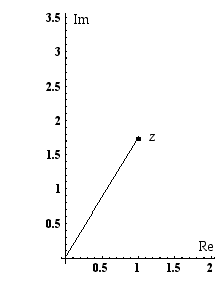
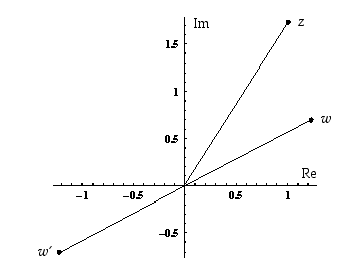
Seuraavasssa kuvassa ovat luvut 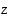 ,
,
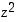 ja
ja 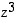 kompleksitasossa.
kompleksitasossa.
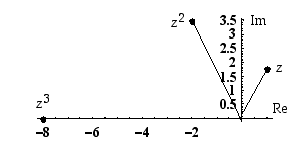
Kuvassa havainnollistuu samalla de Moivren kaava 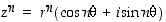 . Esimerkiksi luvun
. Esimerkiksi luvun 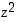 etäisyys origosta (moduli) on luvun
etäisyys origosta (moduli) on luvun 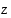 etäisyyden neliö ja luvun
etäisyyden neliö ja luvun 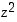 argumentti on kaksinkertainen luvun
argumentti on kaksinkertainen luvun 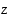 argumenttiin nähden.
argumenttiin nähden.
c) Tiedetään, että 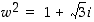 ,
ja kun a)-kohdan perusteella
,
ja kun a)-kohdan perusteella
niin de Moivren kaavaa hyödyntämällä saadaan
[Opiskelutehtävä 10] [Vinkki tehtävään 10]