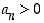 kun
kun 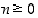 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Väite pätee aloitusluvulle 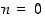 ,
sillä
,
sillä 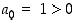 .
.
Oletetaan, että väite 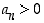 pätee luvulle
pätee luvulle 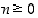 .
.
Seuraavaksi osoitetaan, että väite pätee myös luvulle 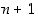 . Tulee siis näyttää, että
. Tulee siis näyttää, että 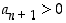 .
.
Tiedetään, että 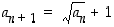 . Oletuksen mukaan
. Oletuksen mukaan 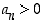 ja tällöin neliöjuuren määritelmän mukaan
ja tällöin neliöjuuren määritelmän mukaan 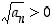 ,
joten myös
,
joten myös 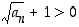 .
.
Nyt on siis osoitettu induktiolla, että esitetty väite pätee kaikille luonnollisille luvuille.
Väite pätee aloitusluvulle 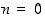 ,
sillä
,
sillä 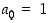 ja
ja 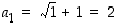 ,
joten
,
joten 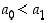 .
.
Seuraavaksi osoitetaan, että väite pätee myös luvulle 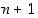 . Tulee siis näyttää, että
. Tulee siis näyttää, että 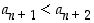 .
.
Tiedetään, että 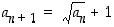 . Oletuksen mukaan
. Oletuksen mukaan 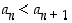 . Koska neliöjuurifunktio on aidosti kasvava (eli "neliöjuuri suuremmasta luvusta on suurempi kuin neliöjuuri pienemmästä luvusta"), niin
. Koska neliöjuurifunktio on aidosti kasvava (eli "neliöjuuri suuremmasta luvusta on suurempi kuin neliöjuuri pienemmästä luvusta"), niin 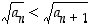 ja tällöin luonnollisesti
ja tällöin luonnollisesti 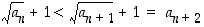 . Näin ollen on saatu näytettyä, että
. Näin ollen on saatu näytettyä, että 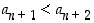 .
.
Induktiotodistuksen mukaan väite siis pätee kaikille luonnollisille luvuille.
Väite pätee aloitusluvulle 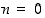 ,
sillä
,
sillä 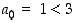 .
.
Seuraavaksi osoitetaan, että väite pätee myös luvulle 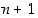 . Tulee siis näyttää, että
. Tulee siis näyttää, että 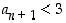 .
.
Tiedetään, että 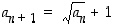 . Oletuksen mukaan
. Oletuksen mukaan 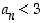 ,
joten neliöjuurifunktion aidon kasvavuuden perusteella
,
joten neliöjuurifunktion aidon kasvavuuden perusteella 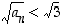 ja tällöin luonnollisesti
ja tällöin luonnollisesti 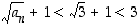 . Siten
. Siten 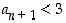 .
.
Induktiotodistuksen mukaan väite siis pätee kaikille luonnollisille luvuille.
[Opiskelutehtävä 1] [Vinkki tehtävään 1]