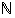 osajoukolle
osajoukolle 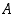 pätevät ehdot
pätevät ehdot
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Luonnollisilla luvuilla on yhteen- ja kertolaskuominaisuuksien lisäksi seuraava hyvin tärkeä ja luonnollisen tuntuinen ominaisuus, joka matematiikassa kuitenkin joudutaan ottamaaan aksioomaksi.
Jos luonnollisten lukujen 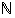 osajoukolle
osajoukolle 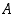 pätevät ehdot
pätevät ehdot
(b) ehdosta 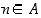 seuraa aina, että myös
seuraa aina, että myös 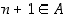 ,
,
sisältää joukko 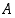 kaikki luonnolliset luvut eli
kaikki luonnolliset luvut eli 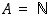 .
.
Tämän aksiooman perusteella voidaan määritellä, mitä tarkoitetaan ns. induktiivisella päättelyllä.
Lause 1.2.2. (Induktiopäättely)
Olkoon 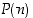 jokin luonnollisesta luvusta
jokin luonnollisesta luvusta 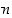 riippuva väite, jolle
riippuva väite, jolle
(b) jokaiselle 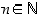 siitä, että
siitä, että 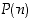 pätee, seuraa että
pätee, seuraa että 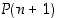 pätee.
pätee.
Todistus. Tulos seuraa induktioaksioomasta, kun luonnollisten lukujen osajoukoksi valitaan joukko 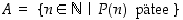 .
.
Induktiopäättely eli induktiotodistus voidaan aloittaa muustakin luvusta kuin nollasta. Silloin tarkasteltava väite saadaan voimaan aloitusluvusta alkaen.
Osoitetaan, että kaikille positiivisille luonnollisille luvuille 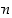 pätee ns. Gaussin kaava
pätee ns. Gaussin kaava
Todistetaan tämä luonnollisesta luvusta 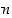 riippuva väite induktiolla. Aloitusluvulle
riippuva väite induktiolla. Aloitusluvulle 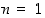 väite pätee, koska
väite pätee, koska 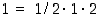 (yhtälön vasemmalla puolella ajatellaan olevan typistetyn yhden alkion summan).
(yhtälön vasemmalla puolella ajatellaan olevan typistetyn yhden alkion summan).
Oletetaan sitten, että väite pätee luvulle 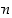 ,
ja osoitetaan, että se pätee myös luvulle
,
ja osoitetaan, että se pätee myös luvulle 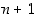 . Koska
. Koska
voidaan ensimmäinen sulkulauseke korvata oletuksen mukaisella summaustuloksella. Siten
mikä osoittaakin, että väitetty kaava pätee myös luvulle 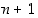 . Induktiopäättelyn mukaan Gaussin summakaava pätee kaikille positiivisille luonnollisille luvuille.
. Induktiopäättelyn mukaan Gaussin summakaava pätee kaikille positiivisille luonnollisille luvuille.
Opiskeluvideo: S1: Induktiotodistus 

Induktiopäättelyä käsitellään enemmän diskreetin matematiikan kurssilla (ks. esimerkiksi sen kurssikirjaa Saarimäki: Diskreettiä ja äärellistä matematiikkaa).
Induktiopäättely mahdollistaa myös ns. induktiiviset eli rekursiiviset määrittelyt: jos jokin asia tai käsite määritellään nollalle (tai muulle aloitusluvulle) ja sen jälkeen sitä suuremmille luonnollisille luvuille edellisen luvun määrittelyyn vedoten, tulee kyseinen asia tai käsite määriteltyä kaikille luonnollisille luvuille.
Luvun 2 potenssit voidaan määritellä seuraavasti. Asetetaan ensin, että 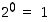 ,
ja sen jälkeen, että
,
ja sen jälkeen, että 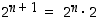 ,
kun
,
kun 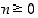 . Silloin potenssit tulevat määritellyiksi kaikilla luonnollisilla luvuilla.
. Silloin potenssit tulevat määritellyiksi kaikilla luonnollisilla luvuilla.
Yleisemmin reaaliluvun 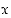 kokonaislukupotenssit määritellään samalla tavalla: Asetetaan, että
kokonaislukupotenssit määritellään samalla tavalla: Asetetaan, että 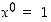 ja
ja 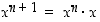 ,
kun
,
kun 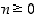 . Erikoisesti luvulle
. Erikoisesti luvulle 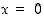 sovitaan, että
sovitaan, että 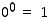 .
.
Opiskelutehtävä 1. (Lukujonon rajoittuneisuus ja monotonisuus)
Määritellään lukujono 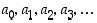 rekursiivisesti:
rekursiivisesti:
Todista induktiolla, että kaikilla 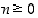 on (a)
on (a) 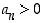 ,
(b)
,
(b) 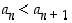 ja (c)
ja (c) 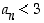 .
.