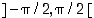Arkustangentti- ja kotangentti

Tangentin käänteisfunktion muodostamiseksi tangentti rajataan avoimelle välille 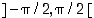, jolloin se on aidosti kasvava ja sen arvojoukko on koko reaalilukujen joukko. Arkustangentti määräytyy siis ehdosta

Arkustangentin derivaatta saadaan käänteisfunktion derivoimissäännöllä. Ku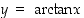n , on

Tangentin ja arkustangentin kuvaajat ovat kuvassa 62.

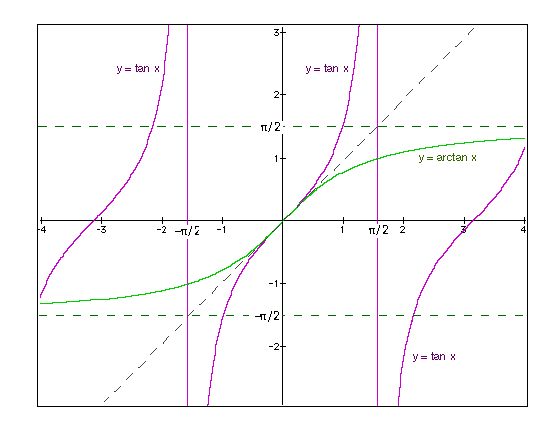
Kuva 62. Tangentin ja arkustangentin kuvaajat

Kun kotangentti rajataan avoimelle välille 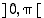, on se tällä välillä aidosti vähenevä ja sen arvojoukko on koko 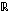. Käänteisfunktio arkuskotangentti määräytyy siten ehdosta

.

Vastaavasti kuin arkuskosini voidaan lausua arkussinin avulla voidaan arkuskotangentti lausua arkustangentin avulla:

Tästä saadaan derivaataksi

Kotangentin ja arkuskotangentin kuvaajat ovat kuvassa 63.

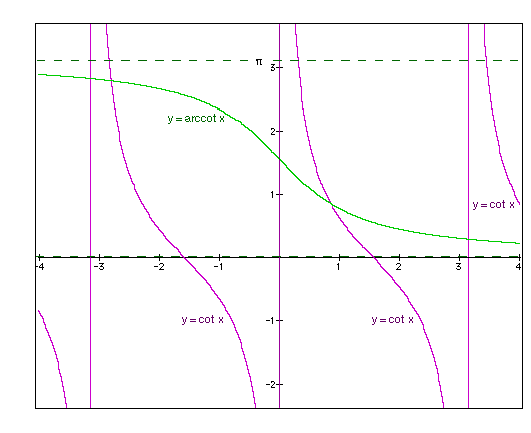
Kuva 63. Kotangentin ja arkuskotangentin kuvaajat

Koska arkusfunktiot ovat trigonometristen funktioiden käänteisfunktioita, niistä käytetään (varsinkin amerikkalaisessa kirjallisuudessa ja myös useissa laskimissa) myös merkintö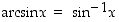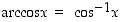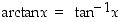jä , , ja 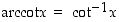.