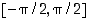 rajoitettuna aidosti kasvava. Tämän rajoittuman käänteisfunktio on arkussini
rajoitettuna aidosti kasvava. Tämän rajoittuman käänteisfunktio on arkussini 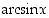 (käytetään myös merkintää
(käytetään myös merkintää 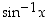 ). Siten
). Siten
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Trigonometriset funktiot sini, kosini, tangentti ja kotangentti ovat kaikki jaksollisia funktioita, joten ne eivät ole bijektioita eikä niillä siten ole käänteisfunktioita. Niillä kaikilla on kuitenkin (peräkkäisiä) välejä, joilla ne ovat monotonisia ja joilla ne saavat jo kaikki mahdolliset arvonsa. Rajaamalla näiden funktioiden määrittelyt sopiville monotonisuusalueille voidaan niille silloin muodostaa käänteisfunktiot. Näitä käänteisfunktioita sanotaan arkusfunktioiksi (tai syklometrisiksi funktioiksi). Seuraavassa käytetyt trigonometristen funktioiden määrittelyalueiden rajaukset ovat yleisimmät, ja niitä sanotaan kyseisten käänteisfunktioiden päähaaroiksi.
Sinifunktio on välille 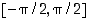 rajoitettuna aidosti kasvava. Tämän rajoittuman käänteisfunktio on arkussini
rajoitettuna aidosti kasvava. Tämän rajoittuman käänteisfunktio on arkussini 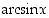 (käytetään myös merkintää
(käytetään myös merkintää 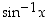 ). Siten
). Siten
Kuvaan 60 on piirretty sinin ja arkussinin kuvaajat (sekä kuvattu käänteisfunktion kuvaajan peilautumista suoran 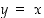 suhteen).
suhteen).
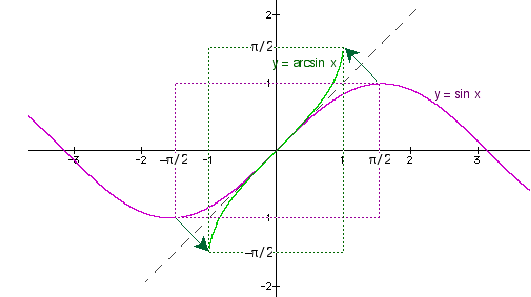
Kuva 60. Sinin ja arkussinin kuvaajat
Määrätään aluksi 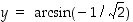 : Koska
: Koska 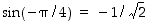 ja
ja 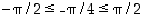 ,
on
,
on 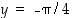 .
.
Entä mitä on 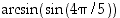 ? Se ei ole
? Se ei ole 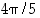 ,
sillä
,
sillä 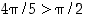 ,
eikä se siten kuulu sinin rajausalueelle. Koska
,
eikä se siten kuulu sinin rajausalueelle. Koska
Määrätään seuraavaksi arkussinin derivaatta. Käänteiskuvauksen derivoimissäännön mukaan arkussini on derivoituva avoimella välillä 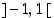 ja jos
ja jos 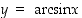 ,
on
,
on
Tässä 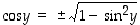 . Rajatulla sinin määrittelyvälillä
. Rajatulla sinin määrittelyvälillä 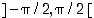 on kosini positiivinen, joten neliöjuuren etumerkki on valittava positiiviseksi. Koska
on kosini positiivinen, joten neliöjuuren etumerkki on valittava positiiviseksi. Koska 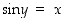 ,
on saatu arkussinin derivaatalle kaava
,
on saatu arkussinin derivaatalle kaava
Arkuskosini on kosinifunktion käänteisfunktio, kun kosini rajoitetaan välillä 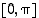 ,
jolla se on aidosti vähenevä. Siis
,
jolla se on aidosti vähenevä. Siis
Arkuskosinin kuvaaja on kuvassa 61.
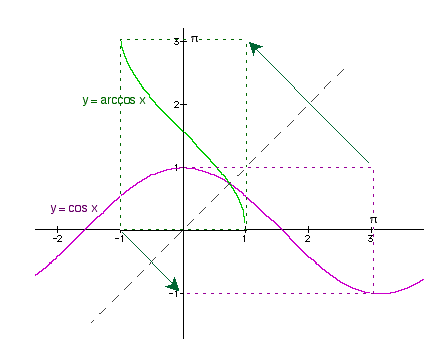
Kuva 61. Kosinin ja arkuskosinin kuvaajat
Arkuskosini voidaan itse asiassa lausua helposti arkussinin avulla. Jos nimittäin 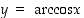 ,
on
,
on 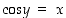 ja
ja 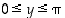 . Tällöin
. Tällöin 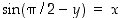 ja
ja 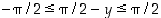 ,
joten
,
joten 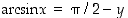 . Näin ollen
. Näin ollen
Tästä nähdään myös, että arkuskosinin derivaatta on vastakkaismerkkinen arkussinin derivaatalle ts.