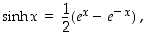
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Eksponenttifunktion avulla määritellään ns. hyperbelifunktiot eli hyperboliset funktiot. Kun trigonometriset funktiot liittyvät geometrisesti ympyrään, liittyvät heperbelifunktiot vastaavasti (suorakulmaiseen yksikkö-)hyperbeliin. Tätä kuvataan tarkemmin määrittelyjen jälkeen (ks. kuva 58). Kuten trigonometrisia funktioita on hyperbelifunktioitakin neljä ja niiden nimetkin ovat analogiset.
Molemmat funktiot ovat kaikkialla määriteltyjä. Määrittelystä näkyy, että sinh on pariton ja cosh on parillinen funktio. Kuvassa 57 on näiden funktioiden kuvaajat. Käyrää 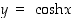 sanotaan myös ketjukäyräksi, sillä päistään ripustettu ohut homogeeninen ketju riippuu tämän käyrän mukaisesti.
sanotaan myös ketjukäyräksi, sillä päistään ripustettu ohut homogeeninen ketju riippuu tämän käyrän mukaisesti.
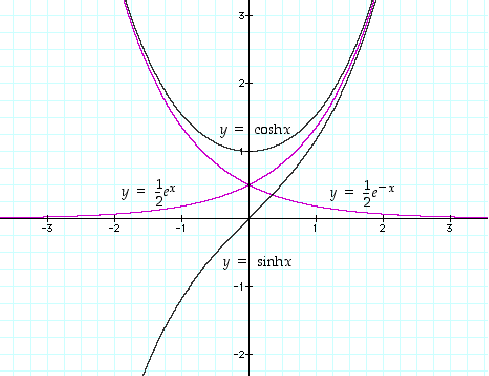
Kuva 57. Hyperbelisinin ja -kosinin kuvaajat
Opiskelutehtävä 37. (Hyperbelisini)
Hyperbelifunktioilla on samantapaisia muokkaussääntöjä kuin trigonometrisilla funktioilla. Seuraavassa on eräitä tärkeimpiä.
Reaaliluvuille 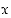 ja
ja 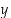 ovat seuraavat voimassa.
ovat seuraavat voimassa.
Todistus. Kohdat (a) ja (b) ovat määrittelyjen perusteella selvät.
Todistetaan sitten kohdan (c) ensimmäinen kaava. Hyperbelisinin ja -kosinin määritelmistä saadaan ratkaistua, että 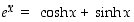 ja
ja 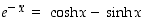 . Näiden avulla saadaan nyt, että
. Näiden avulla saadaan nyt, että
Tämän kohdan toinen kaava todistetaan vastaavasti.
Kohdan (d) kaavat saadaan edellä olevista sijoittamalla 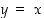 . Kaava (e) taas saadaan funktion
. Kaava (e) taas saadaan funktion 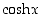 summakaavasta sijoittamalla
summakaavasta sijoittamalla 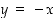 .
.
Edellä olevan lauseen viimeisen kohdan mukaan sellaiset tason pisteet 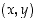 ,
joille
,
joille 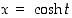 ja
ja 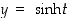 toteuttavat yhtälön
toteuttavat yhtälön 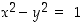 eli ne ovat kyseisellä hyperbelikäyrällä. Tästä nähdään tietty analogia vastaavien trigonometristen funktioiden kanssa. Jos nimittäin
eli ne ovat kyseisellä hyperbelikäyrällä. Tästä nähdään tietty analogia vastaavien trigonometristen funktioiden kanssa. Jos nimittäin 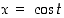 ja
ja 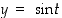 ,
on piste
,
on piste 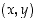 yksikköympyrän
yksikköympyrän 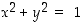 kaarella. Lisäksi parametrin (kulman)
kaarella. Lisäksi parametrin (kulman) 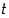 arvolla ympyrästä rajoittuu sektori, jonka pinta-ala on
arvolla ympyrästä rajoittuu sektori, jonka pinta-ala on 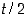 (ks. kuva 58). Voidaan osoittaa, että vastaavasti parametrin (hyperbolisen kulman)
(ks. kuva 58). Voidaan osoittaa, että vastaavasti parametrin (hyperbolisen kulman) 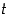 arvolla hyperbelin kaarta vastaa sektori, jonka pinta-ala on myös
arvolla hyperbelin kaarta vastaa sektori, jonka pinta-ala on myös 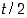 (ks. kuva 58).
(ks. kuva 58).
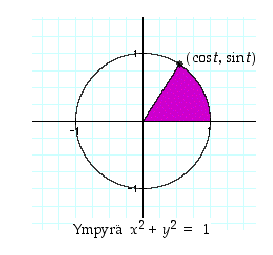
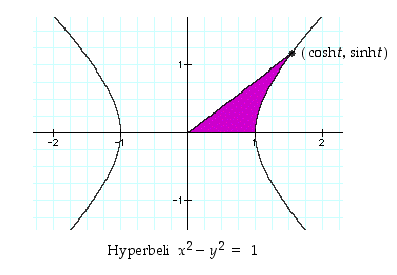
Kuva 58. Ympyräkulma ja hyperbolinen kulma
Koska hyperbelisini ja -kosini määritellään eksponenttifunktion avulla, ovat ne kaikkialla derivoituvia. Lisäksi
Edelleen analogisesti trigonometristen funktioiden kanssa määritellään hyperbelitangentti
Näille funktioille on aina 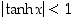 ja
ja 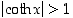 .
.
Hyperbelitangentin ja -kotangentin derivaatat saadaan osamäärän derivoimissäännöillä ja ne ovat
Hyperbelitangentin ja -kotangentin kuvaajat ovat kuvassa 59.
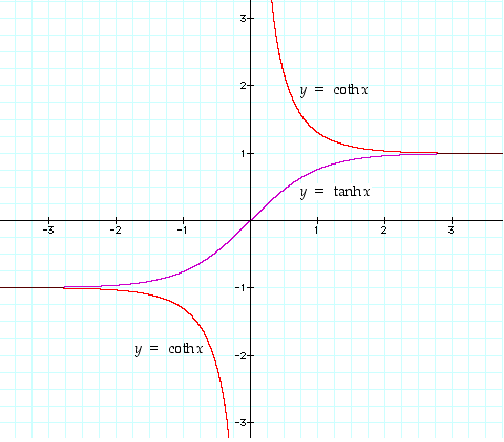
Kuva 59. Hyperbelitangentin ja -kotangentin kuvaajat
Opiskelutehtävä 38. (Hyperbelitangentin raja-arvot)