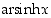Areafunktiot

Hyperbelifunktioilla on, osalla määrittelyalueita rajaten, käänteisfunktiot, joita kutsutaan areafunktioiksi. Määritellään ne seuraavassa.

Hyperbelisinin derivaatta on hyperbelikosini, joka on kaikkialla positiivinen. Hyperbelisini on siten aidosti kasvava koko reaalialueella. Sen arvojoukko on myös koko reaalialue. Sillä on näin ollen kaikkialla määritelty käänteisfunktio, areahyperbelisini 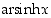, joka määrittyy ehdosta

.

Funktiolle 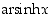voidaan löytää analyyttinen lauseke logaritmifunktion avulla seuraavasti.

Edellä toisen asteen yhtälön ratkaisussa on neliöjuuren etumerkiksi valittava plus-merkki, koska 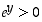. On siis saatu, että

.

Käänteisfunktion derivoimissäännöllä tai derivoimalla edellä oleva lauseke saadaan derivaataksi

Hyperbelikosini ei ole bijektio, mutta positiivisilla arvoilla sen derivaatta 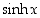on positiivinen, joten se on aidosti kasvava epänegatiivisilla arvoilla. Näille arvoille eli välille 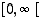rajoitettuna funktion 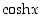arvojoukko on väli 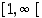ja sillä on silloin käänteisfunktio areahyperbelikosini 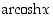, joka määrittyy ehdosta

.

Kuten areahyperbelisinille voidaan areahyperbelikosinille johtaa analyyttinen lauseke

, kun .

Tästä lausekkeesta saadaan derivaataksi

Hyperbelitangentti ja -kotangentti ovat molemmat aidosti monotonisia, joten niillä on käänteisfunktiot, areahyperbelitangentti 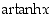ja areahyperbelikotangentti 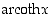. Nämä määräytyvät ehdoista

,

ja

.

Näillekin funktioille on johdettavissa analyyttiset lausekkeet

ja

Molempien funktioiden derivaatoilla on sama lauseke

mutta määrittelyalueet ovat erilaiset, edellisellä se on väli 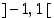ja jälkimmäisellä sen muodostavat välit 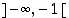ja .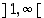

Areafunktiot ovat siis hyperbolisten funktioiden käänteisfunktioita. Tästä syystä (varsinkin amerikkalaisessa kirjallisuudessa ja myös useissa laskimissa) näistä funktioista käytetään myös merkintö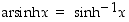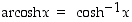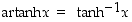jä , , ja 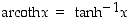.