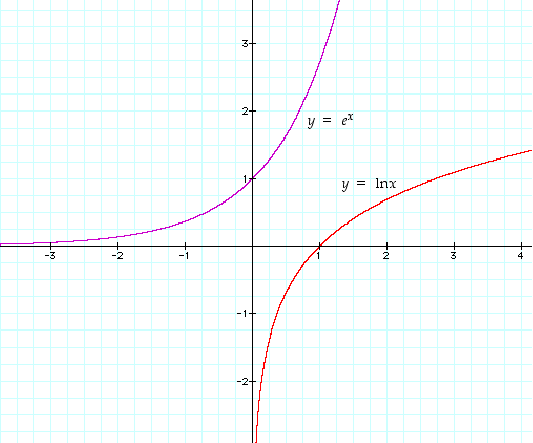Luonnollinen logaritmifunktio
Eksponenttifunktio 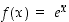 on aidosti kasvava ja kaikkialla derivoituva, jonka arvojoukko on väli
on aidosti kasvava ja kaikkialla derivoituva, jonka arvojoukko on väli  . Sillä on siten aidosti kasvava ja kaikkialla derivoituva käänteisfunktio
. Sillä on siten aidosti kasvava ja kaikkialla derivoituva käänteisfunktio 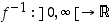 . Tätä sanotaan (luonnolliseksi tai tavalliseksi) logaritmifunktioksi ja merkitään
. Tätä sanotaan (luonnolliseksi tai tavalliseksi) logaritmifunktioksi ja merkitään 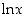 (tai myös
(tai myös 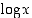 ). Siis
). Siis
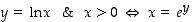 .
.
Erityisesti 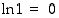 ,
,
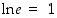 ,
,
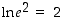 ja yleisesti
ja yleisesti 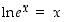 ,
kun
,
kun 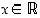 . Vastaavasti
. Vastaavasti 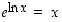 ,
kun
,
kun 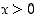 . Seuraavat säännöt periytyvät eksponenttifunktion säännöistä.
. Seuraavat säännöt periytyvät eksponenttifunktion säännöistä.
Lause 6.2.1.
Kun 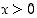 ,
,
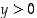 ja
ja 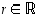 ,
niin
,
niin
(a) 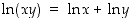 ,
,
(b) 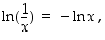
(c) 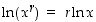 .
.
(d) 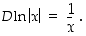
Todistus. Tyyppiä 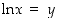 oleva väite voidaan käänteiskuvauksen avulla todistaa osoittamalla, että
oleva väite voidaan käänteiskuvauksen avulla todistaa osoittamalla, että 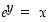 . Tämä periaate huomioiden lauseen kolme ensimmäistä väitettä seuraavat laskuista
. Tämä periaate huomioiden lauseen kolme ensimmäistä väitettä seuraavat laskuista
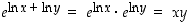 ,
,
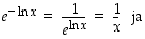
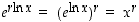 .
.
Kohdan (d) derivoimissäännön todistusta varten olkoon ensin 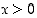 . Käänteisfunktion derivoimissäännön mukaan on silloin
. Käänteisfunktion derivoimissäännön mukaan on silloin
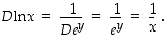
Tapaus 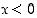 voidaan palauttaa edelliseen tapaukseen merkin vaihdolla. Todistus jätetään opiskelutehtäväksi (tehtävä 33).
voidaan palauttaa edelliseen tapaukseen merkin vaihdolla. Todistus jätetään opiskelutehtäväksi (tehtävä 33).

Opiskelutehtävä 33. (Logaritmifunktion derivaatta)
Osoita, että 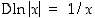 aina, kun
aina, kun 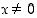 .
.
Vinkki tehtävään 33
Opiskelutehtävä 34. (Logaritmifunktion ääriarvot)
Määrää lausekkeen 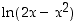 ääriarvot.
ääriarvot.
Vinkki tehtävään 34
Opiskelutehtävä 35. (Yhdistetyn logaritmifunktion derivointi)
Määrää 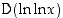 .
.
Vinkki tehtävään 35
Logaritmifunktion ja eksponenttifunktion kuvaajat ovat kuvassa 56.
Kuva 56. Eksponentti- ja logaritmifunktion kuvaajat
Havainnollistus: Logaritmifunktio 
Opiskeluvideo: K4: Funktion käyttäytymisen selvittäminen 

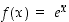 on aidosti kasvava ja kaikkialla derivoituva, jonka arvojoukko on väli
on aidosti kasvava ja kaikkialla derivoituva, jonka arvojoukko on väli 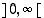 . Sillä on siten aidosti kasvava ja kaikkialla derivoituva käänteisfunktio
. Sillä on siten aidosti kasvava ja kaikkialla derivoituva käänteisfunktio 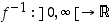 . Tätä sanotaan (luonnolliseksi tai tavalliseksi) logaritmifunktioksi ja merkitään
. Tätä sanotaan (luonnolliseksi tai tavalliseksi) logaritmifunktioksi ja merkitään 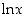 (tai myös
(tai myös 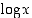 ). Siis
). Siis 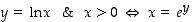 .
. 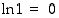 ,
,
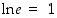 ,
,
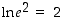 ja yleisesti
ja yleisesti 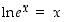 ,
kun
,
kun 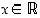 . Vastaavasti
. Vastaavasti 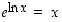 ,
kun
,
kun 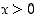 . Seuraavat säännöt periytyvät eksponenttifunktion säännöistä.
. Seuraavat säännöt periytyvät eksponenttifunktion säännöistä. 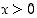 ,
,
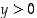 ja
ja 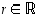 ,
niin
,
niin 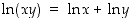 ,
,
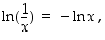
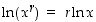 .
. 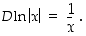
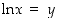 oleva väite voidaan käänteiskuvauksen avulla todistaa osoittamalla, että
oleva väite voidaan käänteiskuvauksen avulla todistaa osoittamalla, että 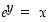 . Tämä periaate huomioiden lauseen kolme ensimmäistä väitettä seuraavat laskuista
. Tämä periaate huomioiden lauseen kolme ensimmäistä väitettä seuraavat laskuista 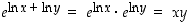 ,
,
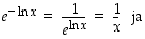
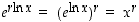 .
. 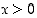 . Käänteisfunktion derivoimissäännön mukaan on silloin
. Käänteisfunktion derivoimissäännön mukaan on silloin 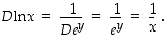
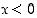 voidaan palauttaa edelliseen tapaukseen merkin vaihdolla. Todistus jätetään opiskelutehtäväksi (tehtävä
voidaan palauttaa edelliseen tapaukseen merkin vaihdolla. Todistus jätetään opiskelutehtäväksi (tehtävä 
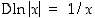 aina, kun
aina, kun 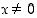 .
. 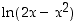 ääriarvot.
ääriarvot.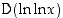 .
.