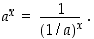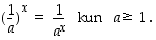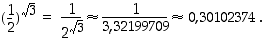Yleinen eksponenttifunktio
Kuten aikaisemmin on todettu, potenssifunktio on muotoa 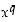 oleva funktio, jossa potenssina on rationaaliluku. Jos
oleva funktio, jossa potenssina on rationaaliluku. Jos 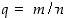 ,
on
,
on 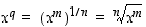 . Kaikki potenssifunktiot on määritelty positiivisille luvuille
. Kaikki potenssifunktiot on määritelty positiivisille luvuille 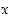 ,
mutta joillekin potensseille määrittelyt voi laajentaa negatiivisillekin luvuille (ks. Potenssi- ja juurifunktio sekä rationaalipotenssit).
,
mutta joillekin potensseille määrittelyt voi laajentaa negatiivisillekin luvuille (ks. Potenssi- ja juurifunktio sekä rationaalipotenssit).
Voisiko potenssifunktion määrittelyä laajentaa myös irrationaalisille potensseille ja siten yleisesti reaalilukupotensseille? Kyllä, käyttäen hyväksi sitä, että täydellisyysaksiooman mukaan reaaliluvut saadaan rationaalilukujen ylärajoina. Määrittely on seuraava.
Olkoon 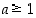 . Reaaliluvulle
. Reaaliluvulle 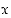 asetetaan, että
asetetaan, että
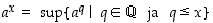 .
.
Määrittely on mielekäs siksi, että jos 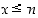 kokonaisluvulle
kokonaisluvulle 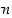 ,
on joukko
,
on joukko 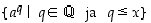 ylhäältä rajoitettu luvulla
ylhäältä rajoitettu luvulla 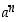 ja siten potenssin
ja siten potenssin 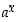 määrittelyssä esiintyvä supremum on olemassa. Näin määriteltyä funktiota
määrittelyssä esiintyvä supremum on olemassa. Näin määriteltyä funktiota 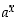 ei enää sanota potenssifunktioksi, vaan yleiseksi tai tarkemmin
ei enää sanota potenssifunktioksi, vaan yleiseksi tai tarkemmin 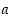 -kantaiseksi eksponenttifunktioksi. Se eroaa potenssifunktiosta siinä, että muuttujana ei ole kantaluku vaan potenssi.
-kantaiseksi eksponenttifunktioksi. Se eroaa potenssifunktiosta siinä, että muuttujana ei ole kantaluku vaan potenssi.
Esimerkki 6.1.1.
Arvioidaan lukua 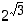 . Koska
. Koska 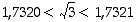 sekä
sekä
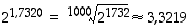 ja
ja 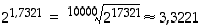 ,
,
pätevät epäyhtälöt 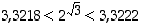 (mahdollisten pyöristysvirheiden takia saatuja arvioita on heikennetty). Siten
(mahdollisten pyöristysvirheiden takia saatuja arvioita on heikennetty). Siten 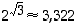 kolmen desimaalin tarkkuudella. Arvioimalla lukua
kolmen desimaalin tarkkuudella. Arvioimalla lukua 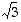 tarkemmin, saadaan potenssille
tarkemmin, saadaan potenssille 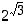 tarkempia likiarvoja. Taskulaskin antaa likiarvoksi
tarkempia likiarvoja. Taskulaskin antaa likiarvoksi 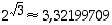 .
.

Kantaluvuille 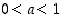 asetetaan, että
asetetaan, että
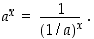
Tällöin pätee, että
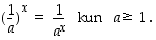
Esimerkiksi
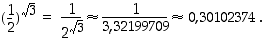
Opiskeluvideo: S4: Eksponenttifunktion arvioiminen murtopotensseilla 

Seuraavassa määrittelemme erityisasemassa olevan eksponenttifunktion, "luonnollisen" eksponenttifunktion. Sitä varten tarvitsemme ensin sen erityisen kantaluvun määrittelyn.
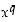 oleva funktio, jossa potenssina on rationaaliluku. Jos
oleva funktio, jossa potenssina on rationaaliluku. Jos 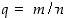 ,
on
,
on 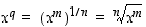 . Kaikki potenssifunktiot on määritelty positiivisille luvuille
. Kaikki potenssifunktiot on määritelty positiivisille luvuille 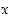 ,
mutta joillekin potensseille määrittelyt voi laajentaa negatiivisillekin luvuille (ks. Potenssi- ja juurifunktio sekä rationaalipotenssit).
,
mutta joillekin potensseille määrittelyt voi laajentaa negatiivisillekin luvuille (ks. Potenssi- ja juurifunktio sekä rationaalipotenssit). 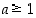 . Reaaliluvulle
. Reaaliluvulle 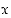 asetetaan, että
asetetaan, että 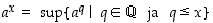 .
. 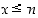 kokonaisluvulle
kokonaisluvulle 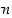 ,
on joukko
,
on joukko 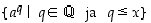 ylhäältä rajoitettu luvulla
ylhäältä rajoitettu luvulla 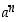 ja siten potenssin
ja siten potenssin 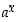 määrittelyssä esiintyvä supremum on olemassa. Näin määriteltyä funktiota
määrittelyssä esiintyvä supremum on olemassa. Näin määriteltyä funktiota 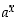 ei enää sanota potenssifunktioksi, vaan yleiseksi tai tarkemmin
ei enää sanota potenssifunktioksi, vaan yleiseksi tai tarkemmin 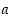 -kantaiseksi eksponenttifunktioksi
-kantaiseksi eksponenttifunktioksi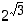 . Koska
. Koska 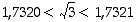 sekä
sekä 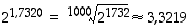 ja
ja 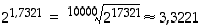 ,
,
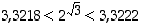 (mahdollisten pyöristysvirheiden takia saatuja arvioita on heikennetty). Siten
(mahdollisten pyöristysvirheiden takia saatuja arvioita on heikennetty). Siten 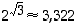 kolmen desimaalin tarkkuudella. Arvioimalla lukua
kolmen desimaalin tarkkuudella. Arvioimalla lukua 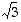 tarkemmin, saadaan potenssille
tarkemmin, saadaan potenssille 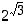 tarkempia likiarvoja. Taskulaskin antaa likiarvoksi
tarkempia likiarvoja. Taskulaskin antaa likiarvoksi 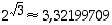 .
. 
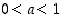 asetetaan, että
asetetaan, että