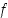 on kahdesti derivoituva välillä
on kahdesti derivoituva välillä 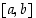 ja päätearvot
ja päätearvot 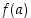 ja
ja 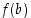 ovat erimerkkiset eli
ovat erimerkkiset eli 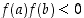 . Tällöin funktiolla
. Tällöin funktiolla 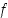 tiedetään olevan nollakohdan
tiedetään olevan nollakohdan 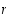 välillä
välillä 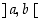 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Numeerisessa ratkaisemisessa lähdetään yleensä jostain ratkaisun alkuarviosta, jota pyritään sitten askel askeleelta parantamaan. Näin saadaan likimääräisten ratkaisujen jono, jossa onnistuneessa tapauksessa joko tarkka ratkaisu tulee vastaan tai joka suppenee kohti tarkkaa ratkaisua.
Yksinkertaisimpia numeerisia menetelmiä nollakohdan etsimiseen on haarukointi: Etsitään ensin kaksi lähellä toisiaan olevaa pistettä, joissa funktio saa erimerkkiset arvot. Jos funktio on jatkuva näiden välillä, on tällä välillä nollakohta. Lasketaan funktion arvo välin puolivälissä. Tämä puolivälipiste on samalla seuraava likiarvo nollakohdaksi. Jos funktion arvo ei ole siinä nolla, valitaan uudeksi väliksi se, jossa merkki muuttuu ja sen puoliväli valitaan uudeksi nollakohdan likiarvoksi. Näin jatketaan, kunnes saadaan nollakohta tai sen likiarvo halutulla tarkkuudella.
Edistyneemmissä numeerisissa ratkaisumenetelmissä nollakohdan likiarvoa pyritään parantamaan nopeammin kuin haarukoinnissa. Hyvää arvausta paremman keinon antaa Newtonin menetelmä, jota kuvataan seuraavassa.
Oletetaan, että funktio 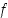 on kahdesti derivoituva välillä
on kahdesti derivoituva välillä 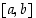 ja päätearvot
ja päätearvot 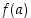 ja
ja 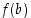 ovat erimerkkiset eli
ovat erimerkkiset eli 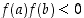 . Tällöin funktiolla
. Tällöin funktiolla 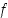 tiedetään olevan nollakohdan
tiedetään olevan nollakohdan 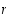 välillä
välillä 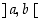 .
.
Valitaan yhtälön 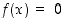 juurelle
juurelle 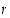 likiarvo
likiarvo 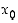 väliltä
väliltä 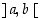 . Pisteeseen
. Pisteeseen 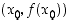 piirretyn tangentin yhtälö on silloin muotoa
piirretyn tangentin yhtälö on silloin muotoa
Sijoittamalla tähän yhtälöön 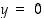 saadaan tangentin ja
saadaan tangentin ja 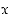 −akselin leikkauspiste
−akselin leikkauspiste
ks. kuva 53.
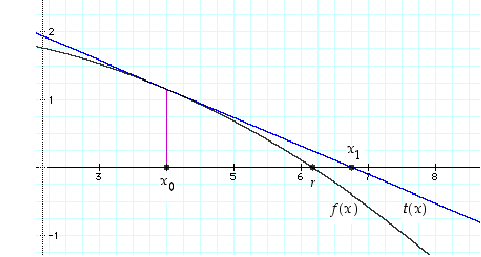
Odotuksena on, ja tietyin edellytyksin myös pätee, että piste 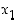 on lähempänä nollakohtaa
on lähempänä nollakohtaa 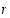 kuin mitä piste
kuin mitä piste 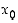 oli. Samalla tavalla määrätään pisteeseen
oli. Samalla tavalla määrätään pisteeseen 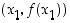 piirretyn tangentin avulla seuraava piste
piirretyn tangentin avulla seuraava piste 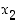 jne. Näin rekursiivisesti jatkamalla saadaan jono
jne. Näin rekursiivisesti jatkamalla saadaan jono 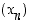 ,
missä
,
missä
Tämän jonon termien laskemista sanotaan Newtonin menetelmäksi.
Jos funktion 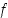 derivaatta on jatkuva ja Newtonin menetelmän mukainen jono
derivaatta on jatkuva ja Newtonin menetelmän mukainen jono 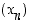 suppenee kohti jotain lukua, on tämä raja-arvo funktion
suppenee kohti jotain lukua, on tämä raja-arvo funktion 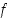 nollakohta.
nollakohta.
Todistus. Olkoon 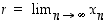 . Tällöin funktion
. Tällöin funktion 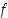 ja sen derivaatan jatkuvuuden perusteella on
ja sen derivaatan jatkuvuuden perusteella on
On huomattava, että edellä oleva lause ilmaisee vain sen, että jos Newtonin menetelmä suppenee, se suppenee jotain nollakohtaa kohti. Se ei ilmaise mitään siitä, milloin tällaista suppenemista tapahtuisi. Newtonin menetelmän suppenemiselle voidaan kyllä johtaa joitakin yleisiä ehtoja. Seuraavassa on eräs, joka on siinä mielessä erityisen hyvä, että se antaa samalla arvion saadun likiarvon virheen suuruudesta. Todistus sivuutetaan.
Oletetaan, että funktion 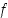 toinen derivaatta on jatkuva sellaisella välillä
toinen derivaatta on jatkuva sellaisella välillä 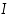 ,
joka sisältää Newtonin menetelmän mukaisen jonon
,
joka sisältää Newtonin menetelmän mukaisen jonon 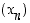 termit sekä funktion
termit sekä funktion 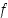 nollakohdan
nollakohdan 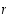 . Oletetaan lisäksi, että on olemassa positiiviset vakiot
. Oletetaan lisäksi, että on olemassa positiiviset vakiot 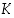 ja
ja 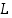 ,
joille
,
joille
Lauseen ehdot (1) ja (2) vaativat, että funktion 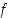 kuvaajan kaltevuus ei ole liian pieni eikä toisaalta muutu liian nopeasti. Jos
kuvaajan kaltevuus ei ole liian pieni eikä toisaalta muutu liian nopeasti. Jos 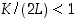 ,
nähdään tuloksesta, että likiarvot
,
nähdään tuloksesta, että likiarvot 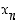 suppenevat varsin nopeasti kohti nollakohtaa
suppenevat varsin nopeasti kohti nollakohtaa 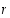 ,
varsinkin sen jälkeen, jos
,
varsinkin sen jälkeen, jos 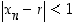 jollekin
jollekin 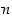 . Yleensä Newtonin menetelmässä nollakohdan likiarvossa oikeiden desimaalien määrää kaksinkertaistuu kullakin askeleella.
. Yleensä Newtonin menetelmässä nollakohdan likiarvossa oikeiden desimaalien määrää kaksinkertaistuu kullakin askeleella.
positiiviselle ratkaisulle likiarvo (katso kuva 54).
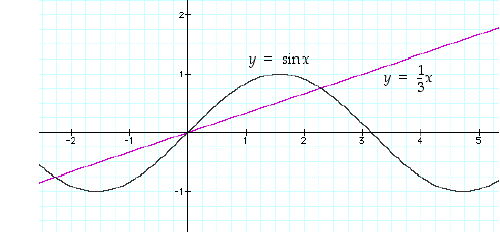
Newtonin menetelmän soveltamista varten tarkastellaan erotusfunktiota 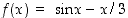 . Sen derivaatta on
. Sen derivaatta on 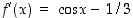 . Käytetään funktion
. Käytetään funktion 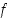 nollakohdalle alkuarvausta
nollakohdalle alkuarvausta 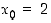 . Newtonin menetelmällä saadaan tämän jälkeen seuraavan taulukon mukaiset likiarvot.
. Newtonin menetelmällä saadaan tämän jälkeen seuraavan taulukon mukaiset likiarvot.
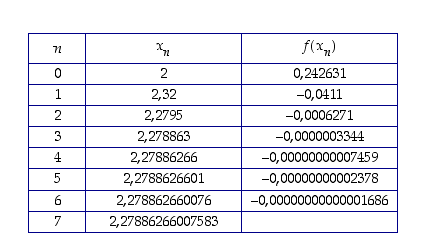
Funktion 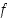 nollakohdan eli yhtälön
nollakohdan eli yhtälön 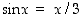 ratkaisun likiarvo on siten
ratkaisun likiarvo on siten 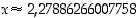 . Kokeile myös alkuarvauksia
. Kokeile myös alkuarvauksia 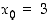 ja
ja 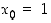 .
.
Esimerkin funktiolle 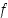 pätee arvio
pätee arvio 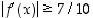 ,
kun
,
kun 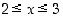 . Lisäksi
. Lisäksi 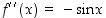 ,
joten
,
joten 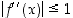 . Siten lauseen 5.4.3 oletukset ovat voimassa vakioin
. Siten lauseen 5.4.3 oletukset ovat voimassa vakioin 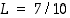 ja
ja 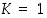 . Näin ollen on
. Näin ollen on 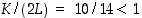 ,
joten Newtonin menetelmän suppeneminen on varsin nopeaa. (Rajaamalla lisää tarkasteluväliä voidaan suhdetta
,
joten Newtonin menetelmän suppeneminen on varsin nopeaa. (Rajaamalla lisää tarkasteluväliä voidaan suhdetta 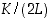 vielä pienentääkin.)
vielä pienentääkin.)
Opiskeluvideo: S3: Funktion nollakohdan arvioiminen Newtonin menetelmällä 

Opiskelutehtävä 31. (Yhtälön ratkaisu numeerisesti)
Määritä yhtälön 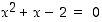 suuremman juuren likiarvo kahden desimaalin tarkkuudella soveltamalla Newtonin menetelmää ja valitsemalla
suuremman juuren likiarvo kahden desimaalin tarkkuudella soveltamalla Newtonin menetelmää ja valitsemalla 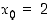 . Piirrä kuva kolmesta ensimmäisestä askeleesta.
. Piirrä kuva kolmesta ensimmäisestä askeleesta.