Raja-arvon määrääminen l'Hospitalin säännöllä
Kun esimerkiksi derivaatan arvoa määrätään erotusosamäärän avulla, joudutaan määräämään sellaisen osamäärän raja-arvo, jossa sekä osoittajan että nimittäjän raja-arvo on nolla. Tällaisia 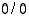 −tilanteita voi tietenkin tulla vastaan muissakin osamäärän raja-arvon määräämisissä. Jos tällaisessa tilanteessa sekä osoittaja että nimittäjä ovat derivoituvia funktioita, voidaan näitä approksimoida tangenttifunktioillaan ja tästä syystä osamäärän raja-arvo voidaan yrittää määrätä kyseisten funktioiden derivaattojen raja-arvojen avulla.
−tilanteita voi tietenkin tulla vastaan muissakin osamäärän raja-arvon määräämisissä. Jos tällaisessa tilanteessa sekä osoittaja että nimittäjä ovat derivoituvia funktioita, voidaan näitä approksimoida tangenttifunktioillaan ja tästä syystä osamäärän raja-arvo voidaan yrittää määrätä kyseisten funktioiden derivaattojen raja-arvojen avulla.
Lause 4.2.1. (l'Hospitalin sääntö)
Olkoot funktiot 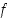 ja
ja 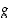 jatkuvia välillä
jatkuvia välillä 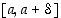 ja derivoituvia vastaavalla avoimella välillä, ja olkoot
ja derivoituvia vastaavalla avoimella välillä, ja olkoot 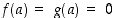 ja
ja 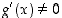 välillä
välillä 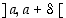 . Jos tällöin on olemassa raja-arvo
. Jos tällöin on olemassa raja-arvo

niin myös
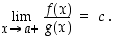
Sääntö pätee vastaavasti myös vasemmanpuolisille raja-arvoille ja (molemminpuolisille) raja-arvoille.
Todistus. Annetaan pisteen 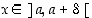 lähestyä pistettä
lähestyä pistettä 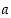 ja selvitetään, mitä kyseisille osamäärille tapahtuu. Lauseen oletuksin funktiot
ja selvitetään, mitä kyseisille osamäärille tapahtuu. Lauseen oletuksin funktiot 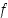 ja
ja 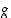 toteuttavat yleistetyn differentiaalilaskennan väliarvolauseen oletukset. Lisäksi
toteuttavat yleistetyn differentiaalilaskennan väliarvolauseen oletukset. Lisäksi 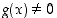 ,
koska
,
koska 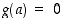 ja derivaatta
ja derivaatta 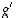 ei ole nolla missään pisteessä. Siten on olemassa piste
ei ole nolla missään pisteessä. Siten on olemassa piste 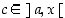 ,
jolle
,
jolle
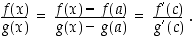
Kun 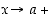 ,
niin myös
,
niin myös 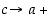 . Tämä huomioimalla seuraa edellisestä lausekkeesta oikeanpuoleisia raja-arvoja koskeva väite.
. Tämä huomioimalla seuraa edellisestä lausekkeesta oikeanpuoleisia raja-arvoja koskeva väite.

Esimerkki 4.2.2.
Määrätään uudestaan jo aikaisemmin esimerkissä 2.2.5 määrätty raja-arvo
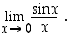
Tässä funktiot 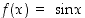 ja
ja 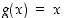 ovat kaikkialla jatkuvia ja derivoituvia sekä
ovat kaikkialla jatkuvia ja derivoituvia sekä 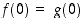 . Lisäksi
. Lisäksi 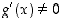 . l'Hospitalin sääntöä voidaan siten soveltaa ja sen mukaan
. l'Hospitalin sääntöä voidaan siten soveltaa ja sen mukaan
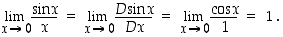

l'Hospitalin säännöllä on useita sellaisia muunnelmia, joita voidaan käyttää epäoleellisten raja-arvojen määräämiseen. Yksi tällainen on seuraava.
Lause 4.2.3. (l'Hospitalin sääntö, 2. versio)
Oletetaan, että on olemassa luku 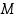 siten, että funktiot
siten, että funktiot 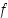 ja
ja 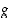 ovat derivoituvia ja
ovat derivoituvia ja 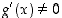 ,
kun
,
kun 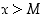 . Jos tällöin
. Jos tällöin
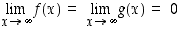 tai
tai 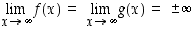
ja
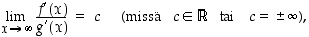
niin myös
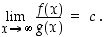
Esimerkki 4.2.4.
Määrätään raja-arvo
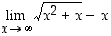
(joka on epämääräistä muotoa 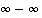 ). Ottamalla lausekkeessa tekijäksi muuttuja
). Ottamalla lausekkeessa tekijäksi muuttuja 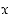 muutetaan lauseke osamäärämuotoon
muutetaan lauseke osamäärämuotoon
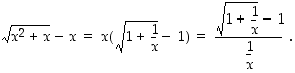
Saadun lausekkeen osoittaja ja nimittäjä toteuttavat nyt edellisen lauseen ehdot. Koska tässä
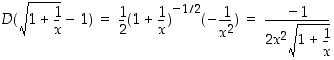
ja
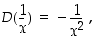
saadaan l'Hospitalin säännön 2. version mukaan
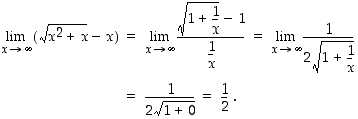

Opiskelutehtävä 23. (Raja-arvon laskeminen l´Hospitalin säännöllä)
Tutki lausekkeen
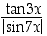
toispuoleisia raja-arvoja pisteessä 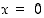 käyttäen l'Hospitalin sääntöä.
käyttäen l'Hospitalin sääntöä.
Vinkki tehtävään 23
Opiskeluvideo: D8: Raja-arvon ratkaiseminen l'Hospitalin säännöllä 

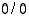 −tilanteita voi tietenkin tulla vastaan muissakin osamäärän raja-arvon määräämisissä. Jos tällaisessa tilanteessa sekä osoittaja että nimittäjä ovat derivoituvia funktioita, voidaan näitä approksimoida tangenttifunktioillaan ja tästä syystä osamäärän raja-arvo voidaan yrittää määrätä kyseisten funktioiden derivaattojen raja-arvojen avulla.
−tilanteita voi tietenkin tulla vastaan muissakin osamäärän raja-arvon määräämisissä. Jos tällaisessa tilanteessa sekä osoittaja että nimittäjä ovat derivoituvia funktioita, voidaan näitä approksimoida tangenttifunktioillaan ja tästä syystä osamäärän raja-arvo voidaan yrittää määrätä kyseisten funktioiden derivaattojen raja-arvojen avulla. 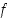 ja
ja 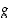 jatkuvia välillä
jatkuvia välillä 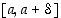 ja derivoituvia vastaavalla avoimella välillä, ja olkoot
ja derivoituvia vastaavalla avoimella välillä, ja olkoot 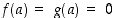 ja
ja 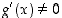 välillä
välillä 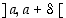 . Jos tällöin on olemassa raja-arvo
. Jos tällöin on olemassa raja-arvo 
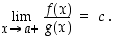
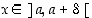 lähestyä pistettä
lähestyä pistettä 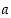 ja selvitetään, mitä kyseisille osamäärille tapahtuu. Lauseen oletuksin funktiot
ja selvitetään, mitä kyseisille osamäärille tapahtuu. Lauseen oletuksin funktiot 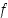 ja
ja 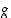 toteuttavat yleistetyn differentiaalilaskennan väliarvolauseen oletukset. Lisäksi
toteuttavat yleistetyn differentiaalilaskennan väliarvolauseen oletukset. Lisäksi 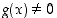 ,
koska
,
koska 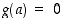 ja derivaatta
ja derivaatta 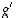 ei ole nolla missään pisteessä. Siten on olemassa piste
ei ole nolla missään pisteessä. Siten on olemassa piste 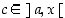 ,
jolle
,
jolle 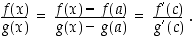
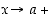 ,
niin myös
,
niin myös 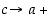 . Tämä huomioimalla seuraa edellisestä lausekkeesta oikeanpuoleisia raja-arvoja koskeva väite.
. Tämä huomioimalla seuraa edellisestä lausekkeesta oikeanpuoleisia raja-arvoja koskeva väite. 
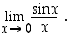
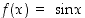 ja
ja 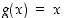 ovat kaikkialla jatkuvia ja derivoituvia sekä
ovat kaikkialla jatkuvia ja derivoituvia sekä 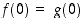 . Lisäksi
. Lisäksi 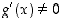 . l'Hospitalin sääntöä voidaan siten soveltaa ja sen mukaan
. l'Hospitalin sääntöä voidaan siten soveltaa ja sen mukaan 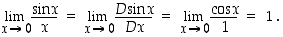

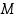 siten, että funktiot
siten, että funktiot 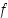 ja
ja 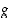 ovat derivoituvia ja
ovat derivoituvia ja 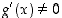 ,
kun
,
kun 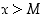 . Jos tällöin
. Jos tällöin 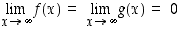 tai
tai 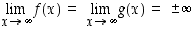
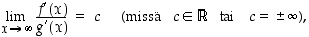
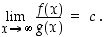
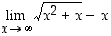
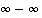 ). Ottamalla lausekkeessa tekijäksi muuttuja
). Ottamalla lausekkeessa tekijäksi muuttuja 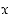 muutetaan lauseke osamäärämuotoon
muutetaan lauseke osamäärämuotoon 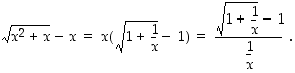
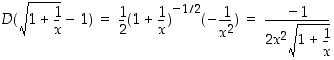
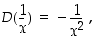
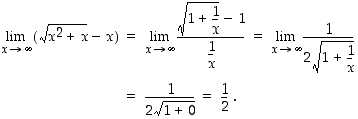

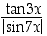
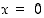 käyttäen l'Hospitalin sääntöä.
käyttäen l'Hospitalin sääntöä. 
