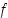 arvoa laskettaessa tarkan arvon
arvoa laskettaessa tarkan arvon 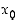 sijasta käytetään likiarvoa
sijasta käytetään likiarvoa 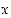 ,
jolloin virhe on siis
,
jolloin virhe on siis 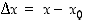 . Tällöin funktion
. Tällöin funktion 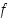 arvoon aiheutuu virhe
arvoon aiheutuu virhe 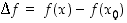 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Sekä funktion differentiaalikehitelmää että väliarvolausetta voidaan käyttää virheenarviointiin. Oletetaan, että funktion 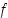 arvoa laskettaessa tarkan arvon
arvoa laskettaessa tarkan arvon 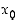 sijasta käytetään likiarvoa
sijasta käytetään likiarvoa 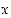 ,
jolloin virhe on siis
,
jolloin virhe on siis 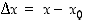 . Tällöin funktion
. Tällöin funktion 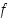 arvoon aiheutuu virhe
arvoon aiheutuu virhe 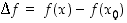 .
.
Jos funktio 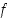 on derivoituva pisteessä
on derivoituva pisteessä 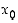 ,
saadaan sen differentiaalikehitelmästä, että
,
saadaan sen differentiaalikehitelmästä, että
Tästä saadaan (pienille virheille 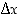 ) tuttu tangenttiarvio
) tuttu tangenttiarvio
Mikäli 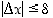 ,
saadaan funktion arvolle virhearvio
,
saadaan funktion arvolle virhearvio
Arvioidaan arvoa 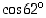 käyttäen hyväksi tunnettua arvoa
käyttäen hyväksi tunnettua arvoa 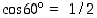 . Funktio
. Funktio 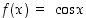 on derivoituva ja
on derivoituva ja 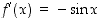 . Koska
. Koska 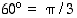 (rad) ja
(rad) ja
pisteen 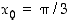 lähellä. Koska edelleen (huomaa, että kulmayksikkönä on käytettävä nyt radiaaneja)
lähellä. Koska edelleen (huomaa, että kulmayksikkönä on käytettävä nyt radiaaneja)
Taskulaskin antaa likiarvon 0,469472.
Väliarvolausetta voidaan puolestaan käyttää virheenarviointiin seuraavasti. Oletetaan, että funktio 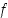 on derivoituva pisteen
on derivoituva pisteen 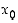 tarkasteluympäristössä. Väliarvolauseen mukaan pätee nyt, että
tarkasteluympäristössä. Väliarvolauseen mukaan pätee nyt, että
jollekin 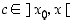 . Oletetaan, että derivaatalle on tiedossa jokin yläraja, ts. olkoon
. Oletetaan, että derivaatalle on tiedossa jokin yläraja, ts. olkoon 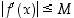 jollakin pisteet
jollakin pisteet 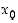 ja
ja 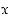 sisältävällä välillä
sisältävällä välillä 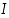 . Tällöin saadaan virhearvio
. Tällöin saadaan virhearvio
Selvitetään, kuinka suuri virhe tehdään, kun luku 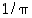 lasketaan käyttäen piin likiarvoa
lasketaan käyttäen piin likiarvoa 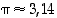 (kun tarkempi piin likiarvo on
(kun tarkempi piin likiarvo on 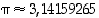 ).
).
Käytetään funktiota 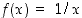 ,
jolle
,
jolle 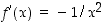 . Koska
. Koska 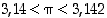 ,
pätee tällä välillä arvio
,
pätee tällä välillä arvio
Kun 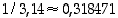 ,
niin on saatu rajat
,
niin on saatu rajat 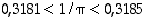 (kun piitä on arvioitu alaspäin, tulee
(kun piitä on arvioitu alaspäin, tulee 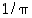 arvioitua ylhäältä päin).
arvioitua ylhäältä päin).
Opiskelutehtävä 24. (Virheenarviointi)
Mitattaessa kuutiota, jonka särmän pituus on 10 m, voidaan tehdä korkeintaan 0,1 m virhe.
(a) Arvioi kuution pinta-alan virhettä differentiaalin avulla.
(b) Arvioi differentiaalilaskennan väliarvolauseen avulla kuinka suuri kuution pinta-alan virhe voi korkeintaan olla.
(c) Kuinka suuri pinta-alan virhe voi korkeintaan olla (tarkka arvo).