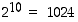 ,
,
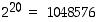 ,
,
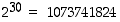 ,
,
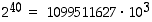 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Oletetaan, että taskulaskin näyttää kymmenen numeroa. Lasketaan sillä seuraavia potensseja:
Huomataan, että luvussa 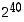 on 13 numeroa, mutta laskin ei näytä niistä kuin kymmenen ensimmäistä. Mitkä olisivat puuttuvat kolme numeroa, ja voisiko ne kuitenkin jotenkin laskea laskimella?
on 13 numeroa, mutta laskin ei näytä niistä kuin kymmenen ensimmäistä. Mitkä olisivat puuttuvat kolme numeroa, ja voisiko ne kuitenkin jotenkin laskea laskimella?
Jätetäänpä luvusta 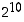 tuhannet pois eli otetaan vain sen kolme viimeistä numeroa käyttöön ja lasketaan sen potensseja:
tuhannet pois eli otetaan vain sen kolme viimeistä numeroa käyttöön ja lasketaan sen potensseja:
Vertaamalla tuloksia edellisiin tuloksiin nähdään, että lukujen 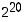 ja
ja 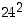 kolme viimeistä numeroa yhtyvät, samoin lukujen
kolme viimeistä numeroa yhtyvät, samoin lukujen 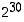 ja
ja 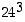 . Olisivatko myös luvun
. Olisivatko myös luvun 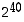 kolme viimeistä numeroa samat kuin luvun
kolme viimeistä numeroa samat kuin luvun 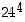 ? Jos olisivat, niin miksi?
? Jos olisivat, niin miksi?
Koska 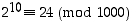 ,
riittäisi ilmeisesti perustella, miksi olisi voimassa myös
,
riittäisi ilmeisesti perustella, miksi olisi voimassa myös 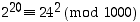 ,
,
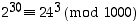 ja
ja 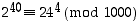 . Pitäisi siis selvittää, milloin kongruenssiyhtälön toisella puolella tehty laskutoimitus voidaan toistaa myös toisella puolella ja saada uusi paikkansa pitävä yhtälö.
. Pitäisi siis selvittää, milloin kongruenssiyhtälön toisella puolella tehty laskutoimitus voidaan toistaa myös toisella puolella ja saada uusi paikkansa pitävä yhtälö.
Tarkastellaan yleisesti kongruenssin muuttumista lukujen yhteen- ja kertolaskuissa. Olkoot sitä varten
ja verrataan keskenään vasemmanpuoleisten lukujen summaa ja tuloa oikeanpuoleisten lukujen summaan ja tuloon. Oletuksen mukaan on 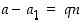 ja
ja 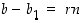 joillekin kokonaisluvuille
joillekin kokonaisluvuille 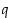 ja
ja 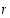 . Tällöin saadaan summien erotukselle esitys
. Tällöin saadaan summien erotukselle esitys
ja vastaavasti tulojen erotukselle
Kokonaislukujen yhteen- ja kertolasku säilyttää siis kongruenttisuuden, ts. kongruenttien lukujen summat ja tulot ovat edelleen keskenään kongruentteja.
Koska 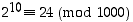 ,
edellä olevan perusteella on
,
edellä olevan perusteella on
Luvun 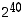 kolme viimeistä numeroa ovat siis 776 (kuten edellä arvailtiinkin).
kolme viimeistä numeroa ovat siis 776 (kuten edellä arvailtiinkin).
Tehtävä. Laskemalla 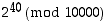 selvitä, onko luvun
selvitä, onko luvun 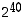 neljänneksi viimeinen numero 6 vai 7. Laskinhan on nimittäin voinut pyöristää viimeisen ilmoittamansa numeron.
neljänneksi viimeinen numero 6 vai 7. Laskinhan on nimittäin voinut pyöristää viimeisen ilmoittamansa numeron.
Vaikka joukon 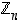 alkiot ovatkin joukkoja, yllä olevan tarkastelun perusteella voimme määritellä sen alkioille
yhteen- ja kertolaskut asettamalla
alkiot ovatkin joukkoja, yllä olevan tarkastelun perusteella voimme määritellä sen alkioille
yhteen- ja kertolaskut asettamalla
Määrittelyt ovat nimittäin silloin siinä mielessä hyvin tehtyjä, että laskutoimitusten tulokset eivät riipu edustajien 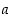 ja
ja 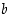 valinnasta.
valinnasta.
mikäli on selvää, mikä moduli 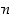 on kyseessä. Samoin ehdon
on kyseessä. Samoin ehdon 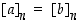 sijasta kirjoitetaan lyhyemmin
sijasta kirjoitetaan lyhyemmin 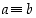 .
.
Muodostetaan joukon 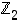 alkioiden yhteen- ja kertolaskutaulukot:
alkioiden yhteen- ja kertolaskutaulukot:
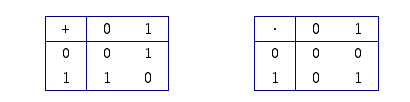
Tällaisessa taulukossa, ns.
operaatiotaulukossa, laskutoimituksen vasemmanpuoleinen alkio (esimerkiksi summassa 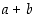 alkio
alkio 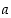 ) luetaan ensimmäiseltä pystysarakkeelta ja oikeanpuoleinen alkio (summassa
) luetaan ensimmäiseltä pystysarakkeelta ja oikeanpuoleinen alkio (summassa 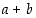 alkio
alkio 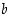 ) ensimmäiseltä vaakariviltä. Tulos (summa
) ensimmäiseltä vaakariviltä. Tulos (summa 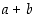 ) luetaan näiden määräämän rivin ja sarakkeen yhtymäkohdasta. Esimerkiksi yllä olevassa yhteenlaskutaulussa summan
) luetaan näiden määräämän rivin ja sarakkeen yhtymäkohdasta. Esimerkiksi yllä olevassa yhteenlaskutaulussa summan 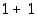 tulos 0 on siis taulukon oikeassa alanurkassa.
tulos 0 on siis taulukon oikeassa alanurkassa.
Tehtävä. Muodosta joukon 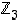 alkioiden yhteen- ja kertolaskutaulukot.
alkioiden yhteen- ja kertolaskutaulukot.
Tehtävä. Laske joukossa 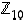 alkioiden 5, 7 ja 9 summa sekä tulo.
alkioiden 5, 7 ja 9 summa sekä tulo.
Koska joukon 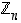 alkioiden yhteen- ja kertolasku määritellään olennaisesti kokonaislukujen vastaavien toimitusten avulla, on seuraava tulos varsin ilmeinen.
alkioiden yhteen- ja kertolasku määritellään olennaisesti kokonaislukujen vastaavien toimitusten avulla, on seuraava tulos varsin ilmeinen.
Joukon 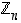 alkioille pätevät samat laskusäännöt kuin kokonaisluvuillekin, ts.
alkioille pätevät samat laskusäännöt kuin kokonaisluvuillekin, ts.
Tässä lauseessa lueteltujen ominaisuuksien perusteella joukko 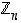 ,
samoin kuin kokonaislukujen joukko
,
samoin kuin kokonaislukujen joukko 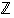 ,
on eräs erikoistapaus yleisemmästä algebrallisesta struktuurista, nimittäin
renkaasta. Tästä syystä joukkoa
,
on eräs erikoistapaus yleisemmästä algebrallisesta struktuurista, nimittäin
renkaasta. Tästä syystä joukkoa 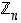 sanotaan myös
jäännösluokkarenkaaksi. Alkiota 0 sanotaan
nolla-alkioksi, alkiota 1
ykkösalkioksi ja alkiota
sanotaan myös
jäännösluokkarenkaaksi. Alkiota 0 sanotaan
nolla-alkioksi, alkiota 1
ykkösalkioksi ja alkiota 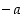 alkion
alkion 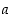 vasta-alkioksi. Alkion ja toisen alkion vasta-alkion summaa
vasta-alkioksi. Alkion ja toisen alkion vasta-alkion summaa 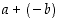 merkitään lyhyemmin erotuksella
merkitään lyhyemmin erotuksella 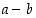 .
.
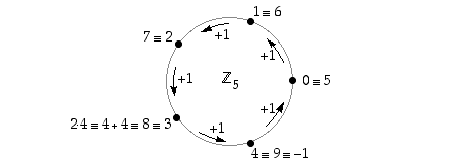
Renkaan 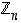 alkioita voidaan graafisesti kuvata ympyrämuotoon sijoitettuna, jolloin näkyy sen 'kiertomaisuus' yhteenlaskun suhteen. Tehdään se, kun
alkioita voidaan graafisesti kuvata ympyrämuotoon sijoitettuna, jolloin näkyy sen 'kiertomaisuus' yhteenlaskun suhteen. Tehdään se, kun 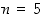 :
:
Opiskelutehtävä 26. (Jäännösluokkarenkaan laskutaulukot)
Muodosta renkaan 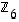 yhteen- ja kertolaskutaulukot.
yhteen- ja kertolaskutaulukot.
Renkaan 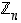 alkioilla lasketaan siis yhteen- ja kertolaskulausekkeita (ja siis polynomeja) aivan kuten kokonaisluvuilla ottamalla vain lisäksi huomioon kongruenttisuudet: negatiiviset luvut ja vähintään luvun
alkioilla lasketaan siis yhteen- ja kertolaskulausekkeita (ja siis polynomeja) aivan kuten kokonaisluvuilla ottamalla vain lisäksi huomioon kongruenttisuudet: negatiiviset luvut ja vähintään luvun 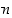 suuruiset luvut voidaan aina korvata jollakin luvuista 0, 1, …,
suuruiset luvut voidaan aina korvata jollakin luvuista 0, 1, …, 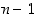 . Kongruenttisuuden huomioiminen saattaa usein helpottaa laskuja huomattavasti.
. Kongruenttisuuden huomioiminen saattaa usein helpottaa laskuja huomattavasti.
Lasketaan potenssi 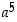 kaikille renkaan
kaikille renkaan 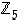 alkioille ja taulukoidaan tulokset:
alkioille ja taulukoidaan tulokset:

Siten saadaan ensi silmäyksellä ehkä yllättävän tuntuinen, identtisesti pätevä yhtälö 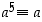 renkaassa
renkaassa 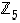 . Toisin sanoen kaikille kokonaisluvuille
. Toisin sanoen kaikille kokonaisluvuille 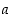 pätee kongruenssi
pätee kongruenssi 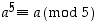 . Niinpä yhtälöllä
. Niinpä yhtälöllä 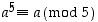 on äärettömän monta kokonaislukuratkaisua, mutta renkaan
on äärettömän monta kokonaislukuratkaisua, mutta renkaan 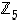 vain viisi (toki kummassakin kaikki mahdolliset alkiot). Yhtälöiden ratkaisemisen kannalta moduloyhtälöt eroavatkin tämän takia tavallisista yhtälöistä!
vain viisi (toki kummassakin kaikki mahdolliset alkiot). Yhtälöiden ratkaisemisen kannalta moduloyhtälöt eroavatkin tämän takia tavallisista yhtälöistä!
Opiskelutehtävä 27. (Kokonaisluvun neliö)
Osoita, että luku 45678901234567890123 ei voi olla minkään kokonaisluvun neliö.
Etsitään vastaus seuraavaan kysymykseen: Mikä on jakojäännös, kun luku 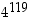 jaetaan luvulla 9?
jaetaan luvulla 9?
Kun jakoyhtälön mukaisesti esitetään 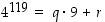 ,
missä
,
missä 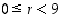 ,
on silloin
,
on silloin 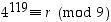 . Määrätäänkin luku
. Määrätäänkin luku 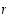 laskemalla renkaassa
laskemalla renkaassa 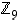 . Koska siinä renkaassa
. Koska siinä renkaassa 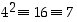 ja edelleen
ja edelleen 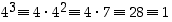 ,
on potenssilaskusääntöjen mukaan
,
on potenssilaskusääntöjen mukaan
Siten 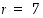 on vastaus esitettyyn kysymykseen.
on vastaus esitettyyn kysymykseen.
Toinen tapa määrätä kysytty potenssiinkorotuksen tulos perustuu potenssin binaariesitykseen. Koska 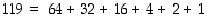 eli
eli 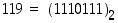 ,
niin
,
niin
Tämän laskemista varten pitää määrätä alkion 4 potenssien potensseja (modulo 9):
Opiskelutehtävä 28. (Potenssille kongruentti luku)
Määrää pienin positiivinen kokonaisluku 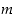 siten, että yhtälö
siten, että yhtälö 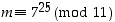 toteutuu.
toteutuu.
Opiskelutehtävä 29. (Jakaminen kongruenssilla)
Osoita modulolaskennan avulla, että luonnollisille luvuille 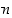 pätee: a)
pätee: a) 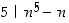 ,
b)
,
b) 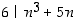 (Vrt. opiskelutehtävä 14).
(Vrt. opiskelutehtävä 14).
Opiskelutehtävä 30. (Peräkkäisten lukujen tulon kahdeksalla jaollisuus)
Osoita, että neljän peräkkäisen kokonaisluvun tulo on aina kahdeksalla jaollinen.
Renkaat 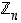 eroavat kokonaislukujen renkaasta
eroavat kokonaislukujen renkaasta 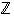 lähinnä parissa ominaisuudessa: Ensinnäkään renkaassa
lähinnä parissa ominaisuudessa: Ensinnäkään renkaassa 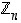 ei päde välttämättä ns. supistamissääntö kuten kokonaisluvuille, joille ehdoista
ei päde välttämättä ns. supistamissääntö kuten kokonaisluvuille, joille ehdoista 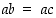 ja
ja 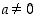 seuraa, että
seuraa, että 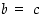 . Toisaalta monilla alkioilla voi olla käänteisalkioita päinvastoin kuin renkaassa
. Toisaalta monilla alkioilla voi olla käänteisalkioita päinvastoin kuin renkaassa 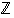 ,
jossa vain luvuilla 1 ja −1 on käänteisluvut. Näitä tilanteita kuvaavat seuraavat esimerkit.
,
jossa vain luvuilla 1 ja −1 on käänteisluvut. Näitä tilanteita kuvaavat seuraavat esimerkit.
Renkaassa 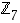 on
on 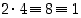 ,
joten alkiot 2 ja 4 ovat toistensa käänteisalkioita siinä mielessä, että niiden tulo on ykkösalkio. Tällaisia tilanteita tarkastellaan lähemmin pykälässä Käänteisalkioista.
,
joten alkiot 2 ja 4 ovat toistensa käänteisalkioita siinä mielessä, että niiden tulo on ykkösalkio. Tällaisia tilanteita tarkastellaan lähemmin pykälässä Käänteisalkioista.
1. Mikä on jakojäännös, kun luku 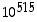 jaetaan luvulla 7?
jaetaan luvulla 7?
2. Määrää auki lasketun luvun 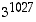 viimeinen numero.
viimeinen numero.
4. Osoita, että neljän peräkkäisen kokonaisluvun summa ei ole koskaan neljällä jaollinen.