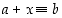 voidaan aina ratkaista; ratkaisu on
voidaan aina ratkaista; ratkaisu on 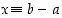 . Mutta muotoa
. Mutta muotoa 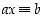 olevalle yhtälölle ratkaiseminen ei ole yhtä selvää.
olevalle yhtälölle ratkaiseminen ei ole yhtä selvää.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Yhteenlaskulla muodostettu yhtälö 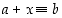 voidaan aina ratkaista; ratkaisu on
voidaan aina ratkaista; ratkaisu on 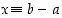 . Mutta muotoa
. Mutta muotoa 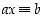 olevalle yhtälölle ratkaiseminen ei ole yhtä selvää.
olevalle yhtälölle ratkaiseminen ei ole yhtä selvää.
Tarkastellaanpa vaikka aluksi yhtälöä 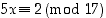 . Voisiko siitä ratkaista muuttujan
. Voisiko siitä ratkaista muuttujan 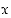 ? Koska moduli 17 on nyt varsin pieni, on tietenkin helppo kokeilla kaikki luvut 0, 1, 2, …, 16 ja siten löytää kaikki ratkaisut. Mutta tämä menettely ei toimi, jos moduli on hyvin suuri.
? Koska moduli 17 on nyt varsin pieni, on tietenkin helppo kokeilla kaikki luvut 0, 1, 2, …, 16 ja siten löytää kaikki ratkaisut. Mutta tämä menettely ei toimi, jos moduli on hyvin suuri.
Yleisemmin toimivan ratkaisumenetelmän johtamiseksi laskemmekin seuraavasti. Ensinnäkin Eukleideen algoritmin mukaisesti on
josta voimme ratkaista luvun 1 muodossa
Käytetään tätä tietoa sitten yhtälön 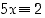 ratkaisemiseen: Kerrotaan se ensin luvulla 7, jolloin saadaan yhtälö
ratkaisemiseen: Kerrotaan se ensin luvulla 7, jolloin saadaan yhtälö
Koskapa päti 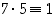 ,
onkin saatu, että
,
onkin saatu, että
Tämä on siis ainoa ratkaisuehdokas (renkaassa 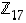 ). Koska toisaalta
). Koska toisaalta
Yllä saatiin välituloksena, että 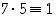 ,
joka siis ilmoittaa, että alkio 7 on alkion 5 'käänteisalkio' renkaassa
,
joka siis ilmoittaa, että alkio 7 on alkion 5 'käänteisalkio' renkaassa 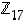 . Tämän löytämisessä taas oli olennaista, että
. Tämän löytämisessä taas oli olennaista, että 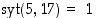 .
.
Sanommekin yleisesti, että renkaassa 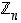 alkio
alkio 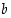 on alkion
on alkion 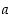 käänteisalkio, jos
käänteisalkio, jos 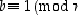 ,
merkitään
,
merkitään 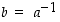 . Alkiota
. Alkiota 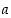 sanotaan silloin myös
kääntyväksi alkioksi. Symmetriasyistä myös alkio
sanotaan silloin myös
kääntyväksi alkioksi. Symmetriasyistä myös alkio 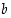 on kääntyvä ja sen käänteisalkio on
on kääntyvä ja sen käänteisalkio on 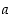 eli
eli 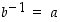 . Erityisesti siten
. Erityisesti siten 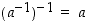 .
.
Seuraava lause ilmoittaa, millaisille alkioille käänteisalkioita löytyy.
Renkaan 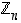 (
(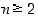 ) alkiolla
) alkiolla 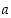 on käänteisalkio täsmälleen silloin, kun luvut
on käänteisalkio täsmälleen silloin, kun luvut 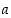 ja
ja 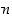 ovat keskenään jaottomat, ts.
ovat keskenään jaottomat, ts. 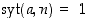 .
.
Todistus. Oletetaan ensin, että 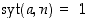 . Pitää löytää siis
. Pitää löytää siis 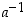 . Oletuksen perusteella
. Oletuksen perusteella 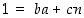 joillekin kokonaisluvuille
joillekin kokonaisluvuille 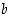 ja
ja 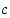 ,
joten
,
joten
Tämän mukaan alkio 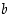 kelpaakin alkion
kelpaakin alkion 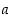 käänteisalkioksi.
käänteisalkioksi.
Oletetaan sitten kääntäen, että 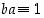 jollekin alkiolle
jollekin alkiolle 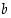 . Silloin
. Silloin 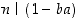 eli
eli 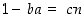 jollekin kokonaisluvulle
jollekin kokonaisluvulle 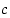 . Jos nyt
. Jos nyt 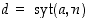 ,
jakaa se luvut
,
jakaa se luvut 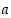 ja
ja 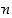 ,
ja siten myös summan
,
ja siten myös summan 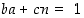 . Niinpä välttämättä
. Niinpä välttämättä 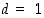 ,
mikä olikin osoitettava.
,
mikä olikin osoitettava.
Renkaan 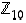 kääntyvät alkiot ovat ne, jotka ovat suhteellisesti jaottomia luvun 10 kanssa, eli siis alkiot 1, 3, 7 ja 9. Lisäksi
kääntyvät alkiot ovat ne, jotka ovat suhteellisesti jaottomia luvun 10 kanssa, eli siis alkiot 1, 3, 7 ja 9. Lisäksi 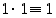 ,
,
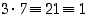 ja
ja 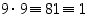 ,
joten näiden käänteisalkiot ovat seuraavat:
,
joten näiden käänteisalkiot ovat seuraavat: 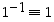 ,
,
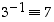 ,
,
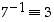 ja
ja 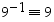 .
.
Ilman muuta pätee aina, että alkio 1, samoin kuin myös −1, on itsensä käänteisalkio, mutta edellisen esimerkin mukaan muullakin alkiolla voi olla tämä ominaisuus.
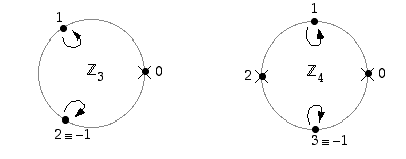
Kuvataan seuraavissa kuvioissa renkaiden 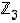 ,
,
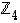 ,
,
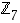 ja
ja 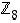 kääntyvät alkiot. Kuvioissa nuolet osoittavat alkion käänteisalkion; ruksi alkion päällä taas merkitsee sitä, että kyseisellä alkiolla ei ole käänteisalkiota.
kääntyvät alkiot. Kuvioissa nuolet osoittavat alkion käänteisalkion; ruksi alkion päällä taas merkitsee sitä, että kyseisellä alkiolla ei ole käänteisalkiota.
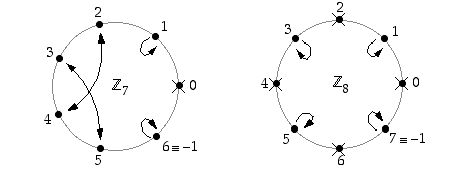
Tehtävä. Määrää renkaiden 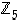 ,
,
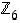 ja
ja 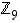 kääntyvät alkiot ja niiden käänteisalkiot.
kääntyvät alkiot ja niiden käänteisalkiot.
Jäännösluokkarenkaissa käänteisalkioita voidaan käyttää yhtälöiden ratkaisemisessa samaan tapaan kuin luvuilla käänteislukuja.
Jos alkio 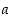 on renkaan
on renkaan 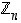 kääntyvä alkio, yhtälöllä
kääntyvä alkio, yhtälöllä 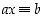 on jokaisella renkaan alkiolla
on jokaisella renkaan alkiolla 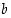 yksikäsitteinen ratkaisu
yksikäsitteinen ratkaisu 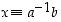 .
.
Todistus. Jos 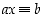 ,
saadaan väitetty ratkaisu kertomalla tämä yhtälö alkiolla
,
saadaan väitetty ratkaisu kertomalla tämä yhtälö alkiolla 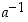 ja huomioimalla, että
ja huomioimalla, että 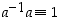 .
.
Toisaalta, jos 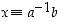 ,
on
,
on 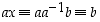 ,
ts. yhtälö
,
ts. yhtälö 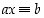 toteutuu.
toteutuu.
Opiskelutehtävä 31. (Käänteisalkiot jäännösluokkarenkaassa)
Määrää kaikki ne renkaan 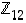 alkiot, joilla on käänteisalkio, ja ilmoita kunkin käänteisalkio.
alkiot, joilla on käänteisalkio, ja ilmoita kunkin käänteisalkio.
Opiskelutehtävä 32. (Yhtälön ratkaiseminen jäännösluokkarenkaassa)
Opiskelutehtävä 33. (Tulon nollasääntö jäännösluokkarenkaassa)
Keksi esimerkki renkaasta 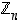 ja sen alkioista
ja sen alkioista 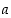 ja
ja 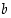 siten, että
siten, että 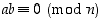 ,
mutta
,
mutta 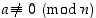 ja
ja 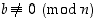 .
.
Jos renkaan 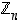 moduli
moduli 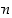 on alkuluku, on siinä renkaassa paljon kääntyviä alkioita.
on alkuluku, on siinä renkaassa paljon kääntyviä alkioita.
Kun 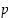 on alkuluku, on jokaisella renkaan
on alkuluku, on jokaisella renkaan 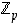 nollasta eroavalla alkiolla käänteisalkio.
nollasta eroavalla alkiolla käänteisalkio.
Väite seuraa siitä, että alkuluvulla on positiivisina tekijöinään vain ykkönen ja se itse, joten jokaiselle renkaan 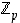 alkiolle
alkiolle 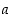 ,
jolle
,
jolle 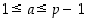 ,
on
,
on 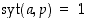 . Lauseen 3.4.1 mukaan sellaisella alkiolla taas on käänteisalkio.
. Lauseen 3.4.1 mukaan sellaisella alkiolla taas on käänteisalkio.
Lause 3.4.6. (Fermat'n pikkulause)
Kun 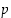 on alkuluku, pätee
on alkuluku, pätee 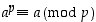 kaikille kokonaisluvuille
kaikille kokonaisluvuille 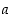 .
.
Todistus. Luvulle 0 väite pätee. Riittää sen jälkeen osoittaa, että 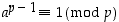 ,
kun
,
kun 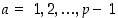 . Kaikilla näillä on edellisen seurauslauseen 3.4.5 mukaan käänteisalkio renkaassa
. Kaikilla näillä on edellisen seurauslauseen 3.4.5 mukaan käänteisalkio renkaassa 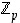 .
.
Olkoon siis 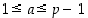 . Tarkastellaan lukuja
. Tarkastellaan lukuja
Kyseiset luvut ovat, paitsi tietysti kokonaislukuina, myös renkaan 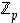 alkioina eri alkioita, sillä jos on
alkioina eri alkioita, sillä jos on 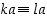 ,
on
,
on 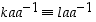 eli
eli 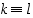 . Siten ne ovat samat kuin alkiot 1, 2, …,
. Siten ne ovat samat kuin alkiot 1, 2, …, 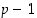 ,
mahdollisesti vain eri järjestyksessä. Niinpä renkaassa
,
mahdollisesti vain eri järjestyksessä. Niinpä renkaassa 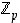 pätee, että
pätee, että
Yhdistämällä yllä olevat tulon 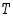 arvot saadaan yhtälö
arvot saadaan yhtälö
Koska jokainen alkioista 1, 2, …, 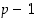 on kääntyvä, yllä oleva yhtälö voidaan supistaa muotoon
on kääntyvä, yllä oleva yhtälö voidaan supistaa muotoon 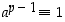 . Olemme siis osoittaneet sen, mitä pitikin.
. Olemme siis osoittaneet sen, mitä pitikin.
Esimerkissä 3.2.5 on todennettu Fermat'n pikkulause renkaassa 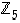 .
.
Tehtävä. Todenna kokeilemalla, että Fermat'n pikkulause pätee renkaassa 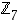 .
.
Fermat'n pikkulause on tärkeä perustulos lukuteoriassa. Sitä voidaan käyttää mm. sen testaamiseen, voiko joku luku 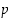 olla alkuluku. Jos nimittäin
olla alkuluku. Jos nimittäin 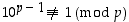 ,
ei
,
ei 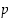 voi olla alkuluku. Fermat'n pikkulause on myös perusta seuraavassa pykälässä (RSA-menetelmä) käsiteltävälle salausmenetelmälle.
voi olla alkuluku. Fermat'n pikkulause on myös perusta seuraavassa pykälässä (RSA-menetelmä) käsiteltävälle salausmenetelmälle.
Pierre de Fermat (1601−1665) oli ranskalainen lakimies, joka harrasti matematiikkaa. Häntä pidetään eräänä todennäköisyyslaskennan pioneerina, mutta tunnetumpi hän on lukuisista lukuteorian tuloksistaan.
Fermat'n suuren lauseen (tai
viimeisen
lauseen) nimellä kulkee eräs hänen väittämistään, jonka mukaan yhtälöllä 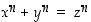 ei ole nollasta eroavia kokonaislukuratkaisuja, kun
ei ole nollasta eroavia kokonaislukuratkaisuja, kun 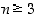 . Fermat ilmoitti aikanaan muistiinpanojensa reunahuomautuksena todistaneensa väittämän, mutta reunatila ei vain riittänyt sen esittämiseen. On syytä epäillä tätä, koska monet jälkipolvetkaan eivät lukuisista yrityksistä huolimatta ole pystyneet todistamaan tai kumoamaan väitettä. Väittämän todistusyrityksiä on vuosisatojen kuluessa ollut lukuisia ja ne ovat johtaneet monien matematiikan alueiden kehitykseen, muidenkin kuin lukuteorian. Todistuksen väittämälle esitti lopultakin englantilainen Andrew Wiles vuonna 1993 ja korjattuna vuonna 1994. Tästä uudentyyppisestä ja Wilesin yli seitsemän vuotta kehittämästä todistuksesta eivät tähänastiset tarkistajat ole löytäneet virhettä ja todistus onkin yleisesti hyväksytty oikeaksi.
. Fermat ilmoitti aikanaan muistiinpanojensa reunahuomautuksena todistaneensa väittämän, mutta reunatila ei vain riittänyt sen esittämiseen. On syytä epäillä tätä, koska monet jälkipolvetkaan eivät lukuisista yrityksistä huolimatta ole pystyneet todistamaan tai kumoamaan väitettä. Väittämän todistusyrityksiä on vuosisatojen kuluessa ollut lukuisia ja ne ovat johtaneet monien matematiikan alueiden kehitykseen, muidenkin kuin lukuteorian. Todistuksen väittämälle esitti lopultakin englantilainen Andrew Wiles vuonna 1993 ja korjattuna vuonna 1994. Tästä uudentyyppisestä ja Wilesin yli seitsemän vuotta kehittämästä todistuksesta eivät tähänastiset tarkistajat ole löytäneet virhettä ja todistus onkin yleisesti hyväksytty oikeaksi.
1. Määrää alkion 7 käänteisalkio renkaassa 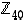 ja ratkaise sitten yhtälö
ja ratkaise sitten yhtälö 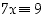 samassa renkaassa.
samassa renkaassa.
2. Osoita, että yleisellä moduloyhtälöllä 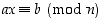 on ratkaisu
on ratkaisu 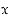 täsmälleen silloin, kun
täsmälleen silloin, kun 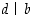 ,
missä
,
missä 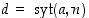 .
.
3. Ratkaise täydellisesti moduloyhtälö 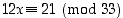 . (Vihje: Selvitä ensin, miten voit moduloyhtälöä yksinkertaistaa huomioiden lukujen yhteiset tekijät.)
. (Vihje: Selvitä ensin, miten voit moduloyhtälöä yksinkertaistaa huomioiden lukujen yhteiset tekijät.)