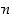voidaan esittää desimaalimuodossa (eli 10−kantaisessa muodossa)
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tunnetusti kokonaisluku on jaollinen luvulla 2 tai luvulla 5, jos sen viimeisellä numerolla on sama ominaisuus. Perustellaan nämä ja keksitään lisää jaollisuustestejä.
Kuten edellisen luvun pykälässä Lukujärjestelmistä todettiin jokainen kokonaisluku 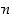voidaan esittää desimaalimuodossa (eli 10−kantaisessa muodossa)
missä luvut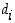 
ovat kokonaislukuja ja 
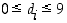. Tämä tarkoittaa luvun 
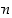esitystä
Esimerkiksi luku 2875 on siis muotoa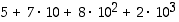 
. Kun muistamme vielä, että luku 
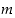on jaollinen luvulla 
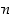täsmälleen silloin, kun 
,
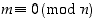saamme kehitettyä useita jaollisuustestejä.
Esimerkki 3.3.1. (2−jaollisuustesti)
Olkoon luvulla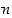 
yllä oleva desimaaliesitys. Tiedämme siis, että 
,
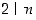jos ja vain jos 
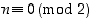. Koska nyt 
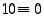ja yleisemmin 
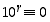kaikilla 
,
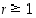saamme seuraavan päättelyketjun:
Tulos on siis todella se, mitä ennakoitiin.
Tehtävä. Osoita vastaavasti 5−jaollisuustesti oikeaksi.
Esimerkki 3.3.2. (9−jaollisuustesti)
Olkoon luvulla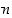 
edelleen sama desimaaliesitys. Laskemme nyt modulo 9. Koska 
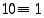ja yleisemmin 
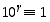kaikilla 
,
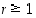saamme seuraavan päättelyketjun:
Luku on siis yhdeksällä jaollinen, jos ja vain jos sen numeroiden summa on yhdeksällä jaollinen. Esimerkiksi luvun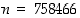 
numerosumma 
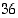on jaollinen luvulla 9, joten myös itse luku 
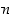on jaollinen luvulla 9.
Tehtävä. Muodosta 3−jaollisuustesti ja osoita se oikeaksi.
1. Muodosta 4−jaollisuustesti ja osoita se oikeaksi.
2. Osoita, että kokonaisluku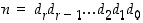 
on jaollinen luvulla 11 täsmälleen silloin, kun summa 
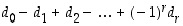on jaollinen luvulla 11.
3. Käyttäen hyväksi sitä, että luku 1001 on jaollinen luvulla 7, johda testi seitsemällä jaollisuudelle.
4. Kokonaisluvun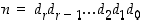 
seitsemällä jaollisuus voidaan testata laskemalla modulo 7 seuraavasti: Kerrotaan vasemmanpuolimmaisin numero 
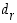luvulla 3 ja lisätään siihen seuraava numero 
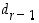. Kerrotaan saatu tulos luvulla 3 ja lisätään siihen seuraava numero 
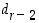. Näin jatketaan, kunnes viimeinen numero 
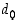on lisätty. Mikäli lopputuloksena on nolla, päätellään, että luku 
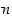on jaollinen luvulla 7. Perustele, miksi tämä menetelmä toimii.
,
. 
